2022-2023学年重庆市北碚区西南大学附中九年级(上)入学数学试卷
发布:2024/9/5 0:0:8
一、选择题。(本大题共12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑.
-
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
组卷:4引用:1难度:0.8 -
2.若代数式
在实数范围内有意义,则x的取值范围为( )2xx-3组卷:112引用:2难度:0.8 -
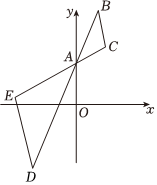 3.如图,在平面直角坐标系中,△ABC以点A为位似中心,放大2倍后得到△ADE.若△ABC的周长为6.则△ADE的周长为( )组卷:78引用:3难度:0.7
3.如图,在平面直角坐标系中,△ABC以点A为位似中心,放大2倍后得到△ADE.若△ABC的周长为6.则△ADE的周长为( )组卷:78引用:3难度:0.7 -
4.估计
的值应在( )3×(22+3)组卷:36引用:2难度:0.7 -
5.按如图所示的程序进行计算,若输入x的值是-1,则输出y的值为-1;若输出y的值为
,则输入x的值是( )13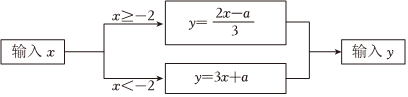 组卷:258引用:1难度:0.5
组卷:258引用:1难度:0.5 -
6.《算学启蒙》中有一道题,原文是:良马日行二百四十里,驽马日行一百二十里.驽马先行一十二日,问良马几何追及之?译文为:跑得快的马每天走240里,跑的慢的马每天走120里.慢马先走12天,快马几天可以追上慢马?设快马x天可以追上慢马,可列方程( )
组卷:2502引用:20难度:0.5 -
7.下列命题是假命题的是( )
组卷:22引用:1难度:0.5 -
8.关于x的方程ax2+3x-2=0有实数根,则a的取值范围是( )
组卷:257引用:5难度:0.5
三、解答题。(本大题共9小题,共86分)解答时每小题必须给出必要的演算过程或推理步骤.请将解答过程书写在答题卡中对应的位置上.
-
24.在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.其中点A(
,0),点C(0,-23),且抛物线的对称轴为直线x=-43,连接AC、BC.3
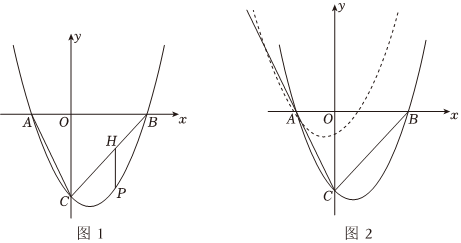
(1)求抛物线的解析式;
(2)如图1,在直线BC的下方抛物线上有一点P,过点P作PH∥y轴交BC于点H,求的最大值以及此时点P的坐标;2PH-22CH
(3)将抛物线y沿射线CA方向平移个单位长度后得到新抛物线y1,点E在新抛物线y1上,点F是原抛物线对称轴上一点,若以点B、C、E、F为顶点的四边形是平行四边形,直接写出点F的坐标,并写出求解其中一个F点的过程.215组卷:99引用:1难度:0.1 -
25.如图,在△ABC中,∠ABC=90°,AB=BC,点D为AC中点,点E为线段AB上一点,连接CE、DE,过点D作DG⊥CE交CE于点F,交BC于点G.
(1)如图1,∠BEC=75°,BE=2,求AC的长;
(2)如图2,若∠AED=∠BEC,连接BF,判断线段EF、BF、GF之间的关系,并证明;
(3)如图3,若点E为AB中点,AB=10,将△ADE绕点A旋转得△AD′E′,连接CD′,以CD′为斜边在CD′左侧作等腰直角△CHD′,连接HG,当HG的长度最大时,请直接写出△CHG的面积.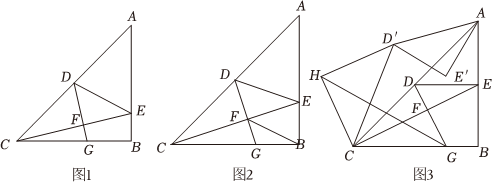 组卷:162引用:2难度:0.1
组卷:162引用:2难度:0.1


