当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省常德市高一（下）期末数学试卷

发布：2024/7/6 8:0:9

1．设集合U={1，2，3，4，5}，M={1，3，5}，N={2，3，4}，则M∩（∁_UN）等于（　　）
A．{3} B．{1，5} C．{1，3，5} D．{1，2，3，4，5}
组卷：171引用：4难度：0.8
解析
2．已知复数z满足（4+3i）z=1+2i,则|z|=（　　）
A．
1
5
B．
5
5
C．
5
D．5
组卷：43引用：4难度：0.8
解析
3．已知角α的顶点在坐标原点，始边在x轴非负半轴上，点P（-6，-8）为角α终边上一点，则cosα=（　　）
A．
-
4
5
B．
3
4
C．
3
5
D．
-
3
5
组卷：213引用：5难度：0.7
解析
4．在正方体ABCD-A₁B₁C₁D₁中，E，F分别是线段BC，C₁D的中点，则异面直线A₁B，EF所成角余弦值是（　　）
A．
2
2
B．
3
3
C．
6
3
D．
3
2
组卷：116引用：5难度：0.7
解析
5．指数函数
y
=
（
b
a
）
x
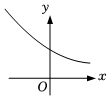的图象如图所示，则二次函数y=ax²+bx图象可能是（　　）
A． B． C． D．
组卷：118引用：6难度：0.8
解析
6．已知平面向量
a
=
（
4
，
2
）
，
b
=
（
1
，
3
）
，则
a
在
b
方向上的投影向量是（　　）
A．（1，3） B．（2，-1） C．（5，5） D．（4，2）
组卷：79引用：5难度：0.7
解析
7．已知实数
a
=
lo
g
2
3
，
b
=
lo
g
3
4
，
c
=
tan
4
π
3
，则（　　）
A．a＞b＞c B．c＞b＞a C．c＞a＞b D．b＞a＞c
组卷：35引用：3难度：0.5
解析

21．如图，在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥面ABCD，AE⊥PB，F为棱PC上一动点．
（1）平面AEF与平面PBC是否相互垂直？如果垂直，请证明；如果不垂直，请说明理由；
（2）若E为PB的中点，求二面角E-AC-B的余弦值．
组卷：88引用：3难度：0.4
解析
22．已知函数
f
（
x
）
=
lo
g
2
2
+
x
2
-
x
．
（1）判断函数f（x）的单调性并加以证明；
（2）若函数
g
（
x
）
=
|
f
（
x
）
+
4
f
（
x
）
-
b
|
+
b
在区间
[
2
3
，
30
17
]
上的最大值为5，求实数b的取值范围．
组卷：61引用：3难度：0.5
解析

1．设集合U={1，2，3，4，5}，M={1，3，5}，N={2，3，4}，则M∩（∁UN）等于（ ）