2023-2024学年江西省南昌市铁路一中高二（上）月考数学试卷（10月份）

一、单选题（本大题共8小题，共40.0分。每小题列出的选项中，选出符合题目的一项）

• 1．设直线l的方向向量为

  m

  =

  （

  2

  ，-

  1

  ，

  z

  ）

  ，平面a的一个法向量为

  n

  =

  （

  4

  ，-

  2

  ，-

  2

  ）

  ，若直线l∥平面a,则实数z的值为（　　）

  A．-5

  B．5

  C．-1

  D．1
  组卷：261引用：9难度：0.8

  解析

• 2．下列直线中，倾斜角为锐角的是（　　）

  A．x-y+1=0

  B．y=-2x+1

  C．y=1

  D．x=2
  组卷：223引用：7难度：0.9

  解析

• 3．若A（1，2），B（3，m），C（7，m+2）三点共线，则实数m的值为（　　）

  A．-2

  B．2

  C．-3

  D．3
  组卷：40引用：4难度：0.5

  解析

• 4．过点P（1，2），且在两坐标轴上截距相等的直线方程为（　　）

  A．2x-y=0或x+y-3=0	B．2x-y=0
  C．x-2y=0或x+y-3=0	D．x+y-3=0
  组卷：313引用：3难度：0.7

  解析

• 5．已知空间中两点A（1，2，3），B（4，2，a），且|AB|=

  10

  ，则a=（　　）

  A．1或2

  B．1或4

  C．0或2

  D．2或4
  组卷：414引用：9难度：0.9

  解析

• 6．如图所示的菱形ABCD中，AB=2，∠BAD=60°，对角线AC，BD交于点O，将△ABD沿BD折到△A′BD位置，使平面A′BD⊥平面BCD．以下命题：
  
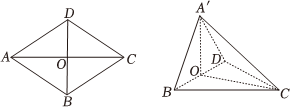
  ①BD⊥A′C；
  ②平面A′OC⊥平面BCD；
  ③平面A′BC⊥平面A′CD；
  ④三棱锥A′-BCD体积为1．
  其中正确命题序号为（　　）

  A．①②③

  B．②③

  C．③④

  D．①②④
  组卷：125引用：5难度：0.5

  解析

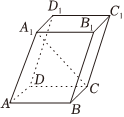• 7．如图，在平行六面体ABCD-A₁B₁C₁D₁中，底面是边长为1的正方形，若∠A₁AB=∠A₁AD=60°，且A₁A=4，则点B到A₁C的距离为（　　）

  A．1

  B． 3 10 10

  C． 10 10

  D． 1 10
  组卷：10引用：1难度：0.6

  解析

四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）

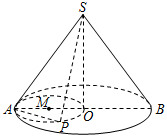• 21．如图所示，圆锥的底面半径为2，其侧面积是底面积的2倍，线段AB为圆锥底面⊙O的直径，在底面内以线段AO为直径作⊙M，点P为⊙M上异于点A，O的动点．
  （1）证明：平面SAP⊥平面SOP；
  （2）当三棱锥S-APO的体积最大时，求二面角A-SP-B的余弦值．
  组卷：199引用：8难度：0.4

  解析

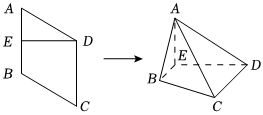• 22．如图，菱形ABCD的边长为2，∠BAD=60°，E为AB的中点．将△ADE沿DE折起，使A到达A'，连接A'B，A'C，得到四棱锥A'-BCDE．
  （1）证明：DE⊥A'B．
  （2）当二面角A'-DE-B在[

  π

  3

  ，

  2

  π

  3

  ]内变化时，求直线A'C与平面A'DE所成角的正弦的最大值．
  组卷：100引用：10难度：0.5

  解析