2023-2024学年江苏省镇江中学附中九年级（上）第一次月考数学试卷

一、填空题（本大题共12小题，每小题2分，共24分）

• 1．方程2x²=3（x-6）化为一般形式为

  ．
  组卷：28引用：2难度：0.8

  解析

• 2．若x=-1是关于x的一元二次方程x²+mx-5=0的一个根，则m=

  ．
  组卷：37引用：3难度：0.6

  解析

• 3．若关于x的一元二次方程（k-1）x²+2x-1=0有实数根，则k的取值范围是

  ．
  组卷：735引用：12难度：0.7

  解析

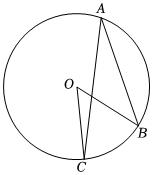• 4．如图，在⊙O中，∠BOC=54°，则∠BAC的度数为

  ．
  组卷：112引用：3难度：0.7

  解析

• 5．已知当x=1时，2ax²+bx的值为3，则当x=-2时，ax²-bx的值为

  ．
  组卷：589引用：3难度：0.8

  解析

• 6．若（a²+b²）（a²+b²-2）=3，则a²+b²=

  ．
  组卷：595引用：14难度：0.9

  解析

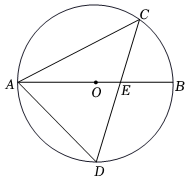• 7．如图，AB是⊙O的直径，弦CD交AB于点E，连接AC，AD．若∠BAC=28°，则∠D=

  °．
  组卷：3328引用：19难度：0.5

  解析

• 8．若直角三角形两直边的长分别为3和4，则此三角形的外接圆半径是

  ．
  组卷：58引用：2难度：0.7

  解析

三、解答题（本大题共8小题，共78分）

• 25．阅读材料：
  材料1：关于x的一元二次方程ax²+bx+c=0（a≠0）的两个实数根x₁，x₂和系数a,b,c,有如下关系：x₁+x₂=-

  b

  a

  ，x₁x₂=

  c

  a

  ．
  材料2：已知一元二次方程x²-x-1=0的两个实数根分别为m,n,求m²n+mn²的值．
  解：∵m,n是一元二次方程x²-x-1=0的两个实数根，
  ∴m+n=1，mn=-1．
  则 m²n+mn²=mn（m+n）=-1×1=-1．
  根据上述材料，结合你所学的知识，完成下列问题：
  （1）应用：一元二次方程2x²+3x-1=0的两个实数根为x₁，x₂，则x₁+x₂=

  ，x₁x₂=

  ．
  （2）类比：已知一元二次方程2x²+3x-1=0的两个实数根为m,n,求m²+n²的值；
  （3）提升：已知实数s,t满足2s²+3s-1=0，2t²+3t-1=0 且s≠t,求

  1

  s

  -

  1

  t

  的值．
  组卷：2235引用：9难度：0.5

  解析

• 26．【问题背景】
  如图1，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．
  小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图2），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=

  2

  CD，从而得出结论：AC+BC=

  2

  CD
  【简单应用】
  （1）在图1中，若AC=

  2

  ，BC=2

  2

  ，则CD=

  ．
  （2）如图3，AB是⊙O的直径，点C、D在⊙O上，

  ˆ

  AD

  =

  ˆ

  BD

  ，若AB=13，BC=12，求CD的长．
  【拓展规律】
  （3）如图4，∠ACB=∠ADB=90°，AD=BD，若AC=m,BC=n（m＜n），求CD的长（用含m,n的代数式表示）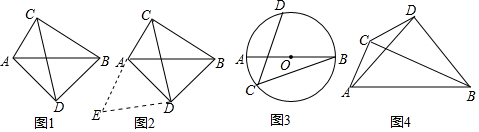
  
  组卷：624引用：15难度：0.1

  解析