当前位置：试卷中心 > 试卷详情

2023-2024学年山西省大同市八年级（上）段考数学试卷（一）

发布：2024/9/13 12:0:8

1．下列图案中，属于全等形的是（　　）
A． B．
C． D．
组卷：26引用：2难度：0.7
解析
2．在△ABC中，若∠B=∠C=30°，则∠A的度数为（　　）
A．90° B．120° C．130° D．150°
组卷：74引用：1难度：0.8
解析
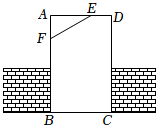3．如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是（　　）
A．两点之间的线段最短
B．长方形的四个角都是直角
C．长方形是轴对称图形
D．三角形有稳定性
组卷：3763引用：73难度：0.9
解析
4．三角形外角和是（　　）
A．540° B．360° C．180° D．90°
组卷：73引用：3难度：0.8
解析
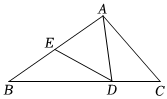5．如图，在△ABC中，D，E分别为BC，AB上的点，则以D为顶点的三角形的个数为（　　）
A．3 B．4 C．5 D．6
组卷：324引用：3难度：0.8
解析
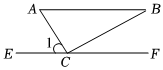6．如图，已知△ABC，点C在EF上，∠A：∠B：∠ACB=2：1：3，若AB∥EF，则∠1的度数为（　　）
A．50° B．55° C．56° D．60°
组卷：28引用：2难度：0.7
解析
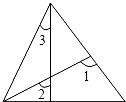7．如图，∠1、∠2、∠3的大小关系为（　　）
A．∠2＞∠1＞∠3 B．∠1＞∠3＞∠2 C．∠3＞∠2＞∠1 D．∠1＞∠2＞∠3
组卷：420引用：52难度：0.9
解析

22．问题情境数学活动课上，老师提出了如下问题：如图，在△ABC中，AB=AC，P是BC上一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点B作BF⊥AC，垂足为F，连接AP．
【特例探究】
（1）如图1，当P为BC边的中点时，利用面积之间的关系可以发现线段PD，PE，BF之间的数量关系为
．
【深入探究】
（2）如图2，当P为BC边上的任意一点时，（1）中的数量关系是否仍然成立？若成立，请加以证明；若不成立，请写出成立的数量关系，并说明理由．
【拓展探究】
（3）如图3，当点P在BC边的延长线上时，
①试猜想线段PD，PE，BF之间的数量关系，并证明你的猜想．
②当S_△ABC=10，AB=5，PE=2时，线段PD的长为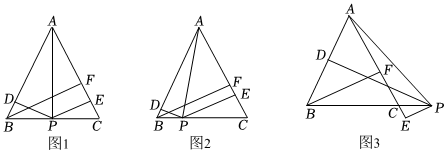
．
组卷：135引用：1难度：0.5
解析
23．（1）如图1，将△ABC沿着DE第一次折叠，顶点B落在△ABC的内部点O处，试探究∠1+∠2与∠B之间的数量关系，并说明理由．
（2）如图2，将△ABC沿着FG第二次折叠，顶点C恰好与点O重合，若∠A=85°，∠5=62°，求∠1+∠3的度数．
（3）如图3，将△ABC沿着GH第三次折叠，顶点A恰好与点O重合，若∠A=α，∠5=β，用含α，β的代数式表示∠6-（∠1+∠AGO）．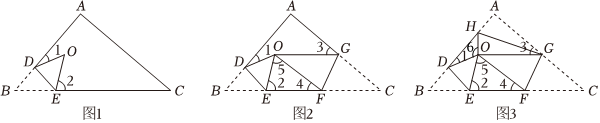
组卷：32引用：1难度：0.5
解析