2023年吉林大学附中中考数学四模试卷
发布：2024/7/1 8:0:9
一、选择题（每小题3分，共24分）
-
1．如图是长春市2022年12月连续四天的天气预报信息，其中日温差最大的一天是（ ）
12月14日 12月15日 12月16日 12月17日 
-13～-20℃
晴-16～-19℃
晴-11～-19℃
晴-14～-20℃
多云组卷：175引用：1难度：0.8 -
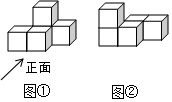2．如图①是由大小相同的小正方体搭成的几何体，将上层的小正方体平移后得到图②．关于平移前后几何体的三视图，下列说法正确的是（ ）组卷：1305引用：26难度：0.8 -
3．在2022年度中国汽车企业创新指数评价中，一汽解放再次斩获中国汽车（商用车）企业创新排行榜第一名.2022年自主开发智能数据终端，实现车联网用户超过2100000人，2100000这个数用科学记数法表示为（ ）
组卷：20引用：3难度：0.8 -
4．不等式4-x≥2的解集在数轴上表示正确的是（ ）
组卷：394引用：7难度：0.8 -
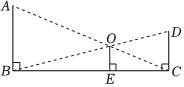5．据《墨经》记载，在两千多年前，我国学者墨子和他的学生做了“小孔成像”实验，阐释了光的直线传播原理．小孔成像的示意图如图所示，光线经过小孔O，物体AB在幕布上形成倒立的实像CD（点A、B的对应点分别是C、D）．若物体AB的高为9cm,小孔O到物体和实像的水平距离BE、CE分别为12cm、9cm,则实像CD的高度为（ ） cm.组卷：815引用：10难度：0.5 -
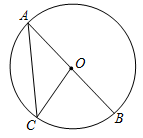6．如图，AB是⊙O的直径，点C在⊙O上，∠OCA=40°，则∠BOC的度数为（ ）组卷：589引用：7难度：0.8 -
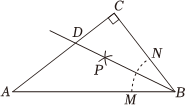7．如图，在Rt△ABC中，∠ACB=90°，按以下步骤作图：①以B为圆心，任意长为半径作弧，分别交BA、BC于M、N两点；②分别以M、N为圆心，以大于的长为半径作弧，两弧相交于点P；③作射线BP，交边AC于D点．若BD=5，点D到AB的距离为3，则△BCD的周长为（ ）12MN组卷：153引用：3难度：0.5 -
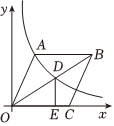8．如图，在平面直角坐标系中，菱形ABCO的顶点O为坐标原点，边CO在x轴正半轴上，∠AOC=60°，反比例函数的图象经过点A，且交菱形对角线BO于点D，DE⊥x轴于点E，则CE长为（ ）y=3x（x＞0）组卷：219引用：1难度：0.6
三、解答题（本大题共10小题，共78分）
-
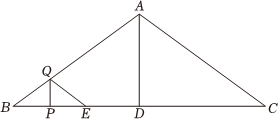23．如图，在△ABC中，AB=AC=10，AD=6，AD⊥BC．点P从点B出发，沿BC方向以每秒4个单位长度的速度向终点C运动，当点P不与点B、C重合时，过点P作PQ⊥BC交折线BA-AC于点Q．PQ将△ABC分成两部分，将所得的三角形沿PQ翻折，得到△PQE．点P的运动时间为t秒．
（1）求BC的长．
（2）当点E与点C重合时，求t的值．
（3）连结QD，当△PQD是等腰三角形时，求t的值．
（4）以点Q为圆心，QE的长为半径作圆，当⊙Q与直线AD相切时，直接写出t的值．组卷：130引用：1难度：0.5 -
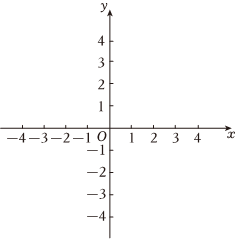24．如图，抛物线y=-x2+bx+c的图象记为G，G与x轴交于点A（-1，0），与y轴相交于点C（0，3），点P是G上一点，横坐标为m.
（1）求抛物线的函数表达式．
（2）若点B是G与x轴的另一个交点，当点P在第一象限时．
①若tan∠PAB=1，求m的值．
②连结BC，点D是线段BC的中点，连结CP，DP，当△CPD面积的最大值时，求m的值．
（3）将G沿射线BC的方向平移个单位长度，得到图象G′，过点P作y轴垂线，交G′的对称轴于点Q，绕点Q将QP逆时针旋转90°得到点M，连结QM，MP，以QM，MP为边作▱PNQM．若G在▱PNQM内部的部分满足y随x的增大而增大，且G′在▱PNQM内部的部分满足y随x的增大而减小时，直接写出m的取值范围．22组卷：196引用：1难度：0.1
