当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省沈阳134中等八校联考八年级（下）月考数学试卷（4月份）

发布：2024/7/16 8:0:9

一.选择题（共10小题，每题2分，共20分

1．如图所示的图案是一些汽车的车标，可以看作由“基本图案”经过平移得到的是（　　）
A． B． C． D．
组卷：287引用：13难度：0.5
解析
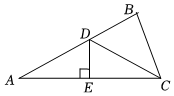2．如图，DE是AC的垂直平分线，CE=4，△BDC的周长为20，则△ABC的周长是（　　）
A．14 B．28 C．30 D．32
组卷：262引用：2难度：0.5
解析
3．不等式
x
-
3
3
＜
2
x
+
1
2
-1变形正确的是（　　）
A．3x-3＜2（2x+1）-1 B．2（x-3）＜3（2x+1）-1
C．2（x-3）＜3（2x+1）-6 D．3x-9＜4x-4
组卷：430引用：6难度：0.7
解析
4．按照下面给定的计算程序，当x=-2时，输出的结果是_____；使代数式2x+5的值小于20的最大整数x是_____．（　　）
A．1，7 B．2，7 C．1，-7 D．2，-7
组卷：350引用：4难度：0.5
解析
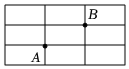5．如图，在小长方形组成的网格中，每个小长方形的长为4，宽为2，A、B两点在网格的格点上，若点C也在网格的格点上，且△ABC是等腰三角形，则满足条件的点C的个数是（　　）
A．2 B．3 C．4 D．5
组卷：123引用：2难度：0.5
解析
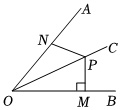6．如图，OC平分∠AOB，点P是射线OC上一点，PM⊥OB于点M，点N是射线OA上的一个动点．若PM=4，则PN的长度不可能是（　　）
A．3 B．4 C．5 D．6
组卷：897引用：7难度：0.7
解析
7．在一次绿色环保知识竞赛中，共有25道题，对于每一道题，答对得5分，答错或不答扣1分，则至少答对多少题，得分才不低于85分？设答对x题，可列不等式为（　　）
A．5x-（25-x）≥85 B．5x+（25-x）≥85
C．5x-（25-x）＞85 D．5x+（25-x）＞85
组卷：681引用：8难度：0.7
解析
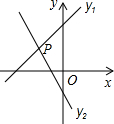8．如图，已知直线y₁=x+m与y₂=kx-1相交于点P（-1，1），则关于x的不等式x+m＞kx-1的解集在数轴上表示正确的是（　　）
A． B． C． D．
组卷：2537引用：19难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

ж三，解答题（第17题6分，第18、19、20、21题各8分，共38

24．在等腰△ABC中，∠B=90°，AM是△ABC的角平分线，过点M作MN⊥AC，垂足为N，∠EMF=135°、将∠EMF绕点M旋转，使∠EMF的两边交直线AB于点E，交直线AC于点F，请解答下列问题：

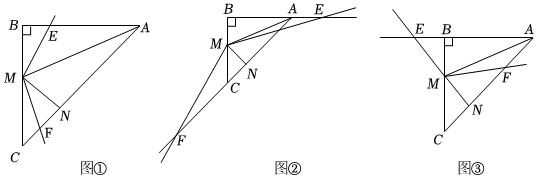
（1）当∠EMF绕点M旋转到如图①的位置时，求证：BE+CF=BM；
（2）当∠EMF绕点M旋转到如图②，图③的位置时，请分别直接写出线段BE，CF，BM之间的数量关系
；
．
（3）在（1）和（2）的条件下，∠BEM=60°，
AB
=
2
+
1
，直接写出CF的长
．
组卷：357引用：3难度：0.5
解析
25．如图1，在平面直角坐标系xOy中，直线MN分别与x轴正半轴、y轴正半轴交于点M、N，且OM=12cm,∠OMN=30°，等边△ABC的顶点B与原点O重合，BC边落在x轴的正半轴上，点A恰好落在线段MN上，如图2，将等边△ABC从图1的位置沿x轴正方向以1cm/s的速度平移，边AB，AC分别与线段MN交于点E、F，在△ABC平移的同时，点P从△ABC的顶点B出发，以2cm/s的速度沿折线B→A→C运动，当点P达到点C时，点P停止运动，△ABC也随之停止平移．设△ABC平移时间为t（s），△PEF的面积为S（cm²）．

（1）等边△ABC的边长是
；
（2）当点P在线段BA上运动时，直接写出S与t的函数关系式
；
（3）点P沿折线B→A→C运动的过程中，是否在某一时刻，使△PEF为等腰三角形？若存在，直接写出此时t值；若不存在，请说明理由．
组卷：258引用：3难度：0.5
解析