2023-2024学年浙江省杭州市精诚联盟高二（上）月考数学试卷（10月份）

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.

• 1．已知向量

  a

  =（1，2，3），

  b

  =（-1，0，1），则

  a

  +2

  b

  =（　　）

  A．（-1，2，5）

  B．（-1，4，5）

  C．（1，2，5）

  D．（1，4，5）
  组卷：313引用：9难度：0.9

  解析

• 2．圆x²+y²-2x+6y+6=0的圆心坐标和半径分别为（　　）

  A．（1，3），2

  B．（1，-3），2

  C．（-1，3），4

  D．（1，-3），4
  组卷：115引用：5难度：0.7

  解析

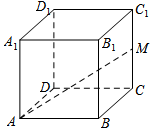• 3．在长方体ABCD-A₁B₁C₁D₁中，M为棱CC₁的中点．若

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则

  AM

  等于（　　）

  A． a + b + 1 2 c	B． a - b + 1 2 c
  C． 1 2 a + 1 2 b + 1 2 c	D． 1 2 a - 1 2 b + 1 2 c
  组卷：264引用：9难度：0.8

  解析

• 4．若过点P（-1，0）的直线与以点

  A

  （

  1

  ，

  2

  ）

  ，

  B

  （

  -

  2

  ，

  3

  ）

  为端点的线段相交，则直线的倾斜角取值范围为（　　）

  A． [ π 4 ， 2 π 3 ]	B． [ π 4 ， π 3 ]
  C． [ 0 ， π 4 ] ∪ [ 2 π 3 ， π ）	D． [ 0 ， π 4 ] ∪ （ π 2 ， 2 π 3 ]
  组卷：847引用：11难度：0.7

  解析

• 5．l₁：a²x-y+a²-3a=0，l₂：（4a-3）x-y-2=0，若l₁∥l₂，则a=（　　）

  A．1

  B．1或2

  C．1或3

  D．3
  组卷：157引用：4难度：0.7

  解析

• 6．已知在正方体ABCD-A₁B₁C₁D₁中，E，F分别为AD，AB的中点，点P在C₁D₁上运动，若异面直线EP，DF所成的角为α，则cosα的最大值为（　　）

  A． 1 5

  B． 2 5

  C． 3 5

  D． 4 5
  组卷：73引用：3难度：0.6

  解析

• 7．已知点A（-4，1）在直线l：（2m+1）x-（m-1）y-m-5=0（m∈R）上的射影为点B，则点B到点P（3，-1）距离的最大值为（　　）

  A． 5 - 10

  B．5

  C． 5 + 10

  D． 5 + 2 10
  组卷：290引用：3难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

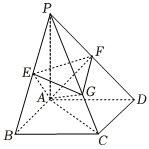• 21．如图，四棱锥P-ABCD的底面为正方形，AB=AP=2，PA⊥平面ABCD，E，F分别是线段PB，PD的中点，G是线段PC上的一点．
  （1）求证：平面EFG⊥平面PAC；
  （2）若直线AG与平面AEF所成角的正弦值为

  1

  3

  ，且G点不是线段PC的中点，求三棱锥E-ABG体积．
  组卷：264引用：6难度：0.4

  解析

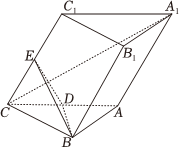• 22．如图，在三棱柱 ABC-A₁B₁C₁ 中，底面是边长为2的等边三角形，CC₁=2，D，E分别是线段AC，CC₁的中点，C₁在平面ABC内的射影为D．
  （1）求证：A₁C⊥平面BDE；
  （2）若点F为线段 B₁C₁上的动点（不包括端点），求锐二面角F-BD-E的余弦值的取值范围．
  组卷：180引用：8难度：0.5

  解析