2022-2023学年浙江省温州市六校八年级(下)第二次学情检测数学试卷
发布:2024/9/19 22:0:8
一、选择题(本大题共10小题,共30分)
-
1.要使二次根式
有意义,则x的值可以为( )x-3组卷:1037引用:37难度:0.9 -
2.下列标志中,可以看作是中心对称图形的是( )
组卷:440引用:40难度:0.9 -
3.某班举办元旦联欢会,班长对全班同学最爱吃哪几种水果这一问题作了调查,班长在确定购买哪一种水果时,最值得关注的统计量是( )
组卷:286引用:4难度:0.8 -
4.下列运算正确的是( )
组卷:522引用:13难度:0.8 -
5.一元二次方程x2-6x-1=0配方后可变形为( )
组卷:1637引用:22难度:0.8 -
6.用反证法证明命题“已知:a∥b,b∥c.求证:a∥c.”,应先假设( )
组卷:65引用:4难度:0.8 -
7.下列说法中,正确的是( )
组卷:1914引用:23难度:0.7 -
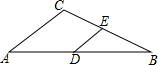 8.如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )组卷:7540引用:75难度:0.9
8.如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )组卷:7540引用:75难度:0.9
三、解答题(本大题共6小题,共46分)
-
23.根据以下素材,探索完成任务,
如何计算工厂生产线数量? 素材1 科学研究表明接种疫苗是战胜新冠病毒的最有效途径.当前居民接种疫苗迎来高峰期,导致相应医疗物资匮乏.某工厂及时引进了一条一次性注射器生产线生产一次性注射器.开工第一天生产400万个. 素材2 经调查发现,1条生产线的最大产量与生产线数量有关,若每增加1条生产线,每条生产线的最大产量将减少20万个/天. 问题解决 任务1 确定最大产量 为了新生产线的适应,前三天1条生产线的产量按日平均增长率50%增加至最大产量,求1条生产线的最大产量. 任务2 拟定初方案 现该厂要保证每天生产一次性注射器4100万个,在增加一定数量生产线的同时又要节省投入(生产线越多,投入越大),求增加的生产线数量. 任务3 优化方案 该厂想使每天生产一次性注射器达到10900万个,若能,应该增加几条生产线?若不能,请说明理由. 组卷:245引用:3难度:0.6 -
24.如图,矩形OABC在平面直角坐标系中,点A在x轴上,OA=8,点C在y轴上,OC=4,点D在BC上,BD=3,点P(0,m)在y轴上,以AD,PD为边向下作平行四边形ADPQ.
(1)求AD的值;
(2)点Q的横坐标是否为定值,请说明理由,并求出点Q的横坐标;
(3)若▱ADPQ的面积被x轴分成1:3两部分,请求出m的值;
(4)若点C关于PD的对称点C′落在x轴上,请求出点Q的坐标.(直接写出答案)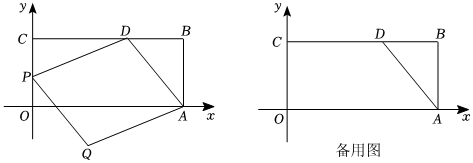 组卷:41引用:1难度:0.3
组卷:41引用:1难度:0.3


