根据以下素材，探索完成任务，
| 如何计算工厂生产线数量？ | ||
| 素材1 | 科学研究表明接种疫苗是战胜新冠病毒的最有效途径．当前居民接种疫苗迎来高峰期，导致相应医疗物资匮乏．某工厂及时引进了一条一次性注射器生产线生产一次性注射器．开工第一天生产400万个. | |
| 素材2 | 经调查发现，1条生产线的最大产量与生产线数量有关，若每增加1条生产线，每条生产线的最大产量将减少20万个/天. | |
| 问题解决 | ||
| 任务1 | 确定最大产量 | 为了新生产线的适应，前三天1条生产线的产量按日平均增长率50%增加至最大产量，求1条生产线的最大产量. |
| 任务2 | 拟定初方案 | 现该厂要保证每天生产一次性注射器4100万个，在增加一定数量生产线的同时又要节省投入（生产线越多，投入越大），求增加的生产线数量. |
| 任务3 | 优化方案 | 该厂想使每天生产一次性注射器达到10900万个，若能，应该增加几条生产线？若不能，请说明理由. |
【答案】任务1：1条生产线的最大产量是900万个；
任务2：增加4条生产线；
任务3：每天生产一次性注射器不能达到10900万个，理由见解答过程．
任务2：增加4条生产线；
任务3：每天生产一次性注射器不能达到10900万个，理由见解答过程．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/9 8:0:8组卷：245引用：3难度：0.6
相似题
-
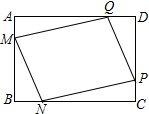1．某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化，为了绿化环境又节省成本．如图，已知矩形的边BC=200m,边AB=a m（a为不大于200的常数），四边形MNPQ的顶点在矩形的边上，且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2
（1）求S关于x的函数关系式，并直接写出自变量x的取值范围；
（2）若a=120，求S的最小值，并求出此时x的值；
（3）若a=200，且每平方米绿化费用需50元，则此时绿化最低费用为万元．发布：2025/6/23 12:30:1组卷：36引用：1难度：0.5 -
2．一公司生产某商品每件成本为20元，经调研发现，该商品在未来40天内的当天销售量m（件）与时间第t（天）满足关系式m=-2t+96；未来40天内，前20天当天的价格y1（元/件）与时间第t（天）的函数式为y1=0.25t+25（1≤t≤20且t为整数），后20天当天的价格y2（元/件）与时间第t（天）的函数式为y2=-0.5t+40（21≤t≤40且t为整数）．
（1）求日销售利润W（元）与时间第t（天）的函数关系式，并写出自变量的取值范围；
（2）请预测未来40天中第 天的日销售利润最大，最大日销售利润是 元．
（3）在实际销售的前20天中，该公司决定每销售一件商品就捐赠a元利润（a＜5）给希望工程，公司通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间第t（天）的增大而增大，求a的取值范围．发布：2025/6/23 11:0:1组卷：116引用：1难度：0.3 -
3．某网店打出促销广告：最潮新款服装30件，每件售价300元．若一次性购买不超过10件时，售价不变；若一次性购买超过10件时，每多买1件，所买的每件服装的售价均降低3元．已知该服装成本是每件200元，设顾客一次性购买服装x件时，该网店从中获利y元．
（1）求y与x的函数关系式，并写出自变量x的取值范围；
（2）顾客一次性购买多少件时，该网店从中获利最多？发布：2025/6/23 13:0:10组卷：4903引用：72难度：0.5
