2022-2023学年广东省广州市天河实验学校九年级(上)月考数学试卷(10月份)
发布:2024/8/24 3:0:9
一、选择题(每小题3分,共30分)
-
1.下列方程中不是一元二次方程的是( )
组卷:113引用:3难度:0.8 -
2.下列函数中,一定是二次函数的是( )
组卷:659引用:3难度:0.8 -
3.对于抛物线y=-2(x+5)2+4,下列说法正确的是( )
组卷:121引用:3难度:0.8 -
4.一元二次方程x2-2x-1=0的根的情况为( )
组卷:3527引用:242难度:0.9 -
5.将y=x2-6x+1化成y=(x-h)2+k的形式,则h+k的值是( )
组卷:794引用:5难度:0.8 -
6.一种药品原价每盒25元,经过两次降价后每盒16元.设两次降价的百分率都为x,则x满足( )
组卷:2935引用:40难度:0.8 -
7.关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根是0,则a的值为( )
组卷:22254引用:347难度:0.9 -
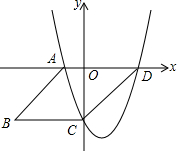 8.如图,抛物线y=x2-2x-3与x轴交于点A、D,与y轴交于点C,四边形ABCD是平行四边形,则点B的坐标是( )组卷:552引用:5难度:0.7
8.如图,抛物线y=x2-2x-3与x轴交于点A、D,与y轴交于点C,四边形ABCD是平行四边形,则点B的坐标是( )组卷:552引用:5难度:0.7
三、解答题(共9个小题,共72分。解答应写出文字说明、证明过程或演算步骤)
-
24.已知抛物线y=x2+bx+c.
(1)如图①,若抛物线与x轴交于点A(3,0),与y轴交点B(0,-3),连接AB.
(Ⅰ)求该抛物线所表示的二次函数表达式;
(Ⅱ)若点P是抛物线上一动点(与点A不重合),过点P作PH⊥x轴于点H,与线段AB交于点M,是否存在点P使得点M是线段PH的三等分点?若存在,请求出点P的坐标;若不存在,请说明理由.
(2)如图②,直线y=x+n与y轴交于点C,同时与抛物线y=x2+bx+c交于点D(-3,0),以线段CD为边作菱形CDFE,使点F落在x轴的正半轴上,若该抛物线与线段CE没有交点,求b的取值范围.43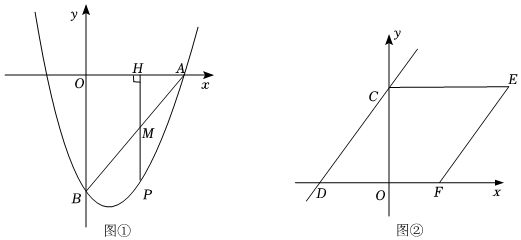 组卷:1502引用:8难度:0.1
组卷:1502引用:8难度:0.1 -
25.如图一所示,在平面直角坐标系中,抛物线y=ax2+2x+c经过点A(-1,0)、B(3,0),与y轴交于点C,顶点为点D.在线段CB上方的抛物线上有一动点P,过点P作PE⊥BC于点E,作PF∥AB交BC于点F.
(1)求抛物线和直线BC的函数表达式.
(2)当△PEF的周长为最大值时,求点P的坐标和△PEF的周长.
(3)若点G是抛物线上的一个动点,点M是抛物线对称轴上的一个动点,是否存在以C、B、G、M为顶点的四边形为平行四边形?若存在,求出点G的坐标,若不存在,请说明理由.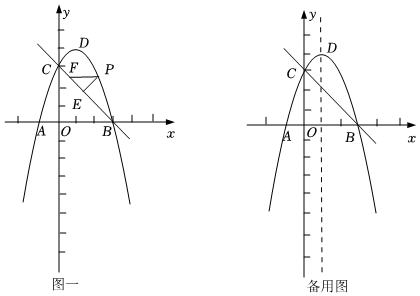 组卷:1493引用:6难度:0.1
组卷:1493引用:6难度:0.1


