当前位置：试卷中心 > 试卷详情

2022-2023学年广东省茂名市电白区八年级（下）期末数学试卷

发布：2024/6/9 8:0:9

1．下列图形中，既是轴对称图形，又是中心对称图形的是（　　）
A． B． C． D．
组卷：279引用：10难度：0.9
解析
2．下列各式不是分式的是（　　）
A．
x
y
B．
y
1
+
y
C．
x
π
D．
2
+
x
a
组卷：136引用：2难度：0.8
解析
3．在▱ABCD中，若∠A+∠C=80°，则∠B的度数是（　　）
A．140° B．120° C．100° D．40°
组卷：395引用：8难度：0.8
解析
4．下列等式从左到右的变形中，属于因式分解的是（　　）
A．（x+1）（x-1）=x²-1 B．x²+2x+1=（x+1）²
C．x²+2x-1=x（x+2）-1 D．x （x-1）=x²-x
组卷：711引用：13难度：0.9
解析
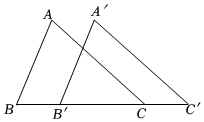5．如图，将△ABC沿BC方向平移2cm得到对应的△A′B′C′．若B′C=4cm,则BC′的长是（　　）
A．6cm B．7cm C．8cm D．10cm
组卷：1476引用：22难度：0.6
解析
6．若一个正多边形的内角和为720°，则这个正多边形的每一个内角是（　　）
A．60° B．90° C．108° D．120°
组卷：1284引用：23难度：0.7
解析
7．如图平行四边形ABCD中，对角线AC，BD相交于点O，点E是CD的中点，若BC=6，则OE的长为（　　）
A．3 B．12 C．8 D．10
组卷：159引用：10难度：0.5
解析

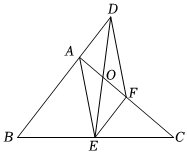22．在Rt△ABC中，∠BAC=90°，E、F分别是BC、AC的中点，延长BA到点D，使AB=2AD，连接DE、DF、AE、EF，AF与DE交于点O．
（1）试说明AF与DE互相平分；
（2）若AB=8，BC=12，求DO的长．
组卷：3625引用：16难度：0.3
解析
23．如图，在平面直角坐标系中，直线y=-3x+3与x轴交于点A，与y轴交于点B，将线段AB绕点A顺时针旋转90°，得到线段AC，过点B，C作直线，交x轴于点D．
（1）点C的坐标为
；求直线BC的表达式；
（2）若点E为线段BC上一点，且△ABE的面积为
5
2
，求点E的坐标；
（3）在（2）的条件下，在平面内是否存在点P，使以点A，B，E，P为顶点的四边形为平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．
组卷：2036引用：5难度：0.1
解析