2023-2024学年天津二中高三（上）开学学情调查数学试卷（一）

一、选择题（共9小题，每题5分，共45分）

• 1．已知集合A={x|y=lg（x+1）}，B={-2，-1，0，1}，则（∁_RA）∩B=（　　）

  A．{-2，-1}

  B．{-2}

  C．{-1，0，1}

  D．{0，1}
  组卷：64引用：6难度：0.9

  解析

• 2．对于实数a,b,c,“a＞b”是“ac²＞bc²”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：848引用：57难度：0.9

  解析

• 3．函数

  f

  （

  x

  ）

  =

  1

  -

  x

  2

  lg

  |

  x

  |

  的图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：526引用：7难度：0.9

  解析

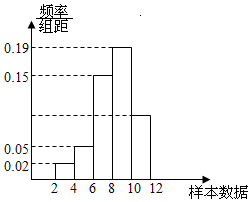• 4．有一个容量为200的样本，其频率分布直方图如图所示，根据样本的频率分布直方图估计，样本数据落在区间[10，12）内的频数为（　　）

  A．18

  B．36

  C．54

  D．72
  组卷：501引用：23难度：0.9

  解析

• 5．长方体的一个顶点上三条棱长是3、4、5，且它的八个顶点都在同一球面上，这个球的体积是（　　）

  A． 125 2 3

  B．125 2 π

  C．50π

  D．125π
  组卷：118引用：10难度：0.9

  解析

• 6．已知x=

  e

  -

  1

  2

  ，y=log₅2，z=ln3，则（　　）

  A．x＜y＜z

  B．z＜x＜y

  C．y＜z＜x

  D．y＜x＜z
  组卷：55引用：5难度：0.7

  解析

三、解答题（共5小题，共75分）

• 19．已知数列{a_n}是公差为2的等差数列，其前8项的和为64，数列{b_n}是公比大于0的等比数列，b₁=3，b₃-b₂=18．
  （1）求数列{a_n}和{b_n}的通项公式；
  （2）记c_n=

  a

  n

  b

  n

  ，n∈N^*，求数列{c_n}的前n项和S_n；
  （3）记d_n=

  a

  n

  +

  2

  -

  1

  a

  n

  a

  n

  +

  1

  b

  n

  ，n∈N*，证明数列{d_n}的前n项和T_n＜

  1

  2

  ．
  组卷：342引用：4难度：0.5

  解析

• 20．已知函数f（x）=（a-

  1

  2

  ）x²+lnx,g（x）=f（x）-2ax（a∈R）．
  （1）当a=0时，
  （i）求曲线y=f（x）在点（2，f（2））处的切线方程；
  （ⅱ）求f（x）的单调区间及在区间[

  1

  e

  ，e]上的最值；
  （2）若对∀x∈（1，+∞），g（x）＜0恒成立，求a的取值范围．
  组卷：190引用：7难度：0.2

  解析