2021-2022学年广东省揭阳市揭西县宝塔学校九年级（上）第三次月考数学试卷

一、选择题（每小题3分，共36分）

• 1．若点A（3，-4）、B（-2，m）在同一个反比例函数的图象上，则m的值为（　　）

  A．-6

  B．6

  C．-12

  D．12
  组卷：398引用：13难度：0.9

  解析

• 2．一元二次方程x（x-1）=0的解是（　　）

  A．x=0

  B．x=1

  C．x=0或x=-1

  D．x=0或x=1
  组卷：930引用：51难度：0.9

  解析

• 3．菱形的两条对角线长分别为6和8，则菱形的周长是（　　）

  A．40

  B．24

  C．20

  D．10
  组卷：193引用：3难度：0.7

  解析

• 4．下列四个几何体中，俯视图为四边形的是（　　）

  A．

  B．

  C．

  D．
  组卷：259引用：82难度：0.9

  解析

• 5．如图，图中的两个转盘分别被均匀地分成5个和4个扇形，每个扇形上都标有数字，同时自由转动两个转盘，转盘停止后，指针都落在奇数上的概率是（　　）

  A． 2 5

  B． 3 10

  C． 3 20

  D． 1 5
  组卷：455引用：34难度：0.9

  解析

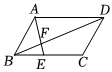• 6．如图，F是平行四边形ABCD对角线BD上的点，BF：FD=1：3，则BE：EC=（　　）

  A． 1 4

  B． 2 3

  C． 1 3

  D． 1 2
  组卷：152引用：5难度：0.7

  解析

• 7．在Rt△ABC中，∠C=90°，AC=12，BC=5，则下列各式中正确的是（　　）

  A．sinA= 12 5

  B．cosA= 12 13

  C．tanA= 12 5

  D．tanA= 12 13
  组卷：7引用：1难度：0.8

  解析

• 8．抛物线y=3x²向右平移1个单位，再向下平移2个单位，所得到的抛物线是（　　）

  A．y=3（x-1）2-2	B．y=3（x+1）2-2
  C．y=3（x+1）2+2	D．y=3（x-1）2+2
  组卷：4578引用：162难度：0.9

  解析

三、解答题

• 24．如图，已知抛物线经过点A（-1，0）、B（3，0）、C（0，3）三点．
  （1）求抛物线的解析式．
  （2）点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N，若点M的横坐标为m,请用m的代数式表示MN的长．
  （3）在（2）的条件下，连接NB、NC，是否存在m,使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．
  组卷：1291引用：28难度：0.3

  解析

• 25．如图，在△ABC中，∠A=90°，AB=3，AC=4，点M，Q分别是边AB，BC上的动点（点M不与A，B重合），且MQ⊥BC，过点M作BC的平行线MN，交AC于点N，连接NQ，设BQ为x.
  （1）试说明不论x为何值时，总有△QBM∽△ABC；
  （2）是否存在一点Q，使得四边形BMNQ为平行四边形，试说明理由；
  （3）当x为何值时，四边形BMNQ的面积最大，并求出最大值．
  组卷：2115引用：3难度：0.3

  解析