如图，在△ABC中，∠A=90°，AB=3，AC=4，点M，Q分别是边AB，BC上的动点（点M不与A，B重合），且MQ⊥BC，过点M作BC的平行线MN，交AC于点N，连接NQ，设BQ为x.
（1）试说明不论x为何值时，总有△QBM∽△ABC；
（2）是否存在一点Q，使得四边形BMNQ为平行四边形，试说明理由；
（3）当x为何值时，四边形BMNQ的面积最大，并求出最大值．
【考点】相似形综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/17 6:0:3组卷：2115引用：3难度：0.3
相似题
-
1．在△ABC和△EDB中，∠C=∠EBD=90°，∠BAC=∠BED=α，点D在线段AC上．
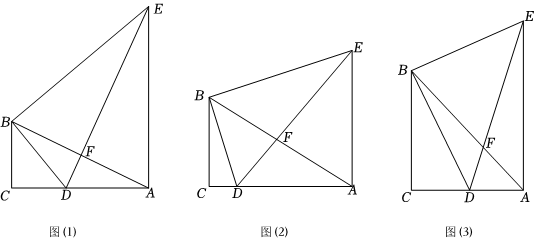
（1）【特例证明】如图（1），当α=30°时，ED⊥AB，证明：AE⊥AC；
（2）【类比探究】如图（2），当α≠30°，点D是线段AC上任一点时，证明：
①△BDF∽△EAF；
②AE⊥AC；
（3）【拓展运用】如图（3），当α=45°时，，AE=12，求BC长．AFBF=35发布：2025/5/21 11:30:1组卷：355引用：4难度：0.2 -
2．如图，在矩形ABCD中，点E为AB上一点，过点D作DP⊥CE于点P，连接DE交AP于点F，点P恰好为CE的中点．
（1）求证：△DEP∽△CEB；
（2）如图1，若，求BEBC=34的值；EFDF
（3）如图2，在（2）的条件下，点G、Q分别为DP、DE上的动点，若CP=5，请直接写出GF+GQ的最小值．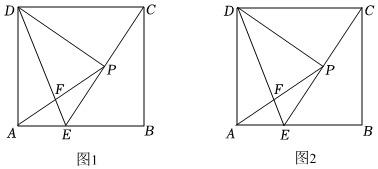
发布：2025/5/21 12:30:1组卷：859引用：1难度：0.2 -
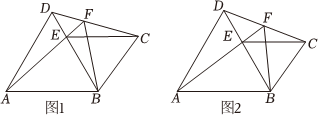3．在四边形ABCD中，AB=AD，对角线BD平分∠ABC，∠ABC=120°，E为BD上一点，EC∥AB，连接AE并延长交DC于点F，连接BF．
（1）如图1，求证：AE=DC；
（2）如图1，若AE=9，DF=4，求BC的长；
（3）如图2．若F为CD的中点，求的值．BCAD发布：2025/5/21 12:30:1组卷：129引用：2难度：0.1
