2021-2022学年广东省江门市高二（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．将3个1和2个0随机排成一行，则2个0相邻的排列方法有（　　）

  A．3种

  B．4种

  C．5种

  D．6种
  组卷：6引用：1难度：0.7

  解析

• 2．直线l：x-y-4=0与圆C：x²+y²=8的位置关系为（　　）

  A．相切

  B．相交

  C．相离

  D．不确定
  组卷：16引用：1难度：0.7

  解析

• 3．在等比数列{a_n}中，a₁+a₃=1，a₄+a₆=-8，则

  a

  10

  +

  a

  12

  a

  5

  +

  a

  7

  =（　　）

  A．-8

  B．16

  C．32

  D．-32
  组卷：418引用：2难度：0.7

  解析

• 4．已知函数f（x）=e^x•lnx,f'（x）为f（x）的导函数，则f′（1）的值为（　　）

  A．0

  B．1

  C． 1 e

  D．e
  组卷：438引用：8难度：0.8

  解析

• 5．从一批含有13件正品，2件次品的产品中不放回地抽3次，每次抽取1件，设抽取的次品数为ξ，则E（5ξ+1）=（　　）

  A．2

  B．1

  C．3

  D．4
  组卷：474引用：8难度：0.7

  解析

• 6．已知曲线y=ax³+xlnx在点（1，a）处的切线方程为y=4x+b,则（　　）

  A．a=1，b=1

  B．a=2，b=-2

  C．a=1，b=-3

  D．a=2，b=2
  组卷：127引用：4难度：0.6

  解析

• 7．将4名北京冬奥会志愿者分配到短道速滑、冰球和冰壶3个项目进行培训，每名志愿者只分配到1个项目，每个项目至少分配1名志愿者，则不同的分配方案共有（　　）

  A．36种

  B．72种

  C．108种

  D．144种
  组卷：135引用：3难度：0.8

  解析

四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知函数f（x）=lnx-ax（a是常数，a＞0）．
  （Ⅰ）当a=2时，求f（x）的单调区间与极值；
  （Ⅱ）若∀x＞0，f（x）＜0，求a的取值范围．
  组卷：39引用：3难度：0.4

  解析

• 22．在某市举办的“中华文化艺术节”知识大赛中，大赛分预赛与复赛两个环节．预赛有4000人参赛．先从预赛学生中随机抽取100人成绩得到如图频率分布直方图：
  
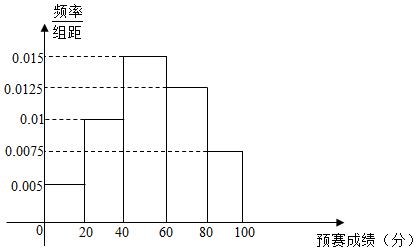
  （1）若从上述样本中预赛成绩不低于60分的学生中随机抽取2人，求至少1人成绩不低于80分的概率；
  （2）由频率分布直方图可以认为该市全体参加预赛的学生成绩Z服从正态分布N（μ，σ²），其中μ可以近似为100名学生的预赛平均成绩，σ²=362，试估计全市参加预赛学生中成绩不低于91分的人数；
  （3）预赛成绩不低于91分的学生可以参加复赛．复赛规则如下：①每人复赛初始分均为100分；②参赛学生可在开始答题前自行选择答题数量n（n＞1），每答一题需要扣掉一定分数来获取答题资格，规定回答第k（k=1，2，…，n）题时扣掉0.2k分；③每答对一题加2分，答错既不加分也不扣分；④答完n题后参赛学生的最后分数即为复赛分数．已知学生甲答对每题的概率为0.75，且各题答对与否相互独立，若甲期望得到最佳复赛成绩，则他的答题数量n应为多少？
  （参考数据

  362

  ≈

  19

  ，若X～N（μ，σ²），则P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-3σ＜X≤μ+3σ）=0.9974）．
  组卷：99引用：3难度：0.5

  解析