2022-2023学年广东省梅州市丰顺县径门中学九年级（上）月考数学试卷（12月份）

一、选择题：本大题共10小题，每小题3分，共30分。

• 1．如图所示的几何体的主视图为（　　）

  A．

  B．

  C．

  D．
  组卷：31引用：2难度：0.8

  解析

• 2．袋中有同样大小的4个小球，其中3个红色，1个白色．从袋中任意地同时摸出两个球，这两个球颜色相同的概率是（　　）

  A． 1 2

  B． 1 3

  C． 2 3

  D． 1 4
  组卷：308引用：23难度：0.9

  解析

• 3．在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是（　　）

  A．AC=BD，AB∥CD，AB=CD	B．AD∥BC，∠A=∠C
  C．AO=BO=CO=DO，AC⊥BD	D．AO=CO，BO=DO，AB=BC
  组卷：1948引用：101难度：0.9

  解析

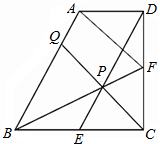• 4．已知直角梯形ABCD中，AD∥BC，∠BCD=90°，BC=CD=2AD，E、F分别是BC、CD边的中点，连接BF、DE交于点P，连接CP并延长交AB于点Q，连接AF．则下列结论不正确的是（　　）

  A．CP平分∠BCD

  B．四边形ABED为平行四边形

  C．CQ将直角梯形分为面积相等的两部分

  D．△ABF为等腰三角形
  组卷：186引用：9难度：0.9

  解析

• 5．如图，顺次连接长方形ABCD四边中点，得四边形EFGH，则这个四边形是（　　）

  A．一般四边形

  B．正方形

  C．菱形

  D．长方形
  组卷：97引用：3难度：0.5

  解析

• 6．在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法．如图所示以线段AB为边作正方形ABCD，取AD的中点E，连接BE，延长DA至F，使得EF=BE，以AF为边作正方形AFGH，则点H即是线段AB的黄金分割点．若记正方形AFGH的面积为S₁，矩形BCIH的面积为S₂，则S₁与S₂的比值是（　　）

  A． 5 + 1 2

  B． 5 - 1 2

  C． 2 2

  D．1
  组卷：324引用：4难度：0.5

  解析

• 7．如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为（　　）

  A．5cm

  B．10cm

  C．20cm

  D．40cm
  组卷：315引用：7难度：0.7

  解析

• 8．如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=

  1

  3

  AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（　　）

  A．①②

  B．②③

  C．①③

  D．①④
  组卷：4031引用：90难度：0.7

  解析

三、解答题：本大题共8小题，第18、19小题6分，第20、21小题7分，第22、23小题8分，第24、25小题10分。

• 24．如图，在平面直角坐标系中，点A、B在x轴上，点C在y轴上，AB=BC=5，AC=8，D为线段AB上一动点，以CD为边在x轴上方作正方形CDEF，连接AE．
  （1）若点B的坐标为（m,0），则m=

  ；
  （2）当BD=

  时，EA⊥x轴；
  （3）当点D由点B运动到点A过程中，点F经过的路径长为

  ；
  （4）当△ADE面积最大时，求出BD的长及△ADE面积最大值．
  组卷：344引用：2难度：0.2

  解析

• 25．对于平面直角坐标系xOy中的动点P和图形N，给出如下定义：如果Q为图形N上一个动点，P，Q两点间距离的最大值为d_max，P，Q两点间距离的最小值为d_min，我们把d_max+d_min的值叫点P和图形N间的“和距离”，记作d（P，图形N）．
  （1）如图1，正方形ABCD的中心为点O，A（3，3）．
  ①点O到线段AB的“和距离”d（O，线段AB）=

  ；
  ②设该正方形与y轴交于点E和F，点P在线段EF上，d（P，正方形ABCD）=7，求点P的坐标．
  （2）如图2，在（1）的条件下，过C，D两点作射线CD，连接AC，点M是射线CD上的一个动点，如果6

  2

  ＜d（M，线段AC）＜6+3

  2

  ，直接写出M点横坐标t取值范围．
  
  组卷：483引用：6难度：0.1

  解析