2022-2023学年吉林省北京师大长春附校八年级（上）期末数学试卷

一、选择题（每题3分，共24分）

• 1．

  4

  的平方根是（　　）

  A．2

  B．±2

  C． 2

  D．± 2
  组卷：2711引用：244难度：0.9

  解析

• 2．下列各数是无理数的是（　　）

  A．0.37

  B．- 1 3

  C．π

  D．0
  组卷：96引用：2难度：0.7

  解析

• 3．下列代数式中，是分式的是（　　）

  A．x+y

  B． x 3

  C．- 1 x

  D． y π
  组卷：174引用：3难度：0.9

  解析

• 4．计算：（-a²）³•a³结果为（　　）

  A．-a9

  B．a9

  C．-a8

  D．a8
  组卷：967引用：4难度：0.6

  解析

• 5．分式

  x

  x

  +

  2

  有意义，x的取值范围是（　　）

  A．x≠0

  B．x≠-2

  C．x≥0

  D．x≥-2
  组卷：231引用：2难度：0.8

  解析

• 6．小明在纸上写下一组数字“20222023”这组数字中2出现的频数为（　　）

  A． 3 8

  B． 5 8

  C．3

  D．5
  组卷：224引用：3难度：0.8

  解析

• 7．如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画圆弧，分别交AB、AC于点D、E，再分别以点D、E为圆心，大于

  1

  2

  DE

  长为半径画圆弧，两弧交于点F，作射线AF交边BC于点G．若CG=8，AB=15，则△ABG的面积是（　　）

  A．150

  B．120

  C．80

  D．60
  组卷：172引用：2难度：0.7

  解析

• 8．如图，一长方体木块长AB=6，宽BC=5，高BB₁=2．一只蚂蚁从木块点A处，沿木块表面爬行到点C₁位置最短路径的长度为（　　）

  A． 89

  B． 85

  C． 125

  D． 80
  组卷：604引用：3难度：0.6

  解析

三、解答题（共78分）

• 23．△ABC与△EBD均为等腰直角三角形，连结AE、CD．
  
  （1）如图1，点E在线段BC上，则AE与CD的数量关系为

  ，位置关系为

  ．
  （2）将△EBD绕点B顺时针旋转至图2位置时，（1）中的两个结论是否还成立，如果成立，请分别证明：如果不成立，请说明理由．
  （3）若在图2中，连结CE、AD，且

  CE

  =

  5

  ，

  AD

  =

  13

  ，则AC²+ED²=

  ．
  组卷：324引用：1难度：0.4

  解析

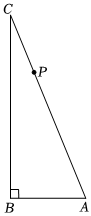• 24．如图，在△ABC中，∠ABC=90°，AC=13，BA=5，点P从点C出发，以每秒3个单位长度的速度沿折线C-A-B运动．设点P的运动时间为t（t＞0）秒．
  （1）BC=

  ．
  （2）求斜边AC上的高线长．
  （3）①当P在AB上时，AP的长为

  ，t的取值范围是

  ．（用含t的代数式表示）
  ②若点P在∠BCA的角平分线上，则t的值为

  ．
  （4）在整个运动过程中，直接写出△PAB是以AB为一腰的等腰三角形时t的值．
  组卷：881引用：2难度：0.5

  解析