2022-2023学年北京市101中学高一（下）期末数学试卷

一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.

• 1．已知a,b∈R，a+3i=（b+i）i（i为虚数单位），则（　　）

  A．a=1，b=-3

  B．a=-1，b=3

  C．a=-1，b=-3

  D．a=1，b=3
  组卷：2546引用：21难度：0.8

  解析

• 2．已知向量

  a

  ，

  b

  满足|

  a

  |=1，|

  b

  |=

  3

  ，|

  a

  -2

  b

  |=3，则

  a

  •

  b

  =（　　）

  A．-2

  B．-1

  C．1

  D．2
  组卷：5562引用：32难度：0.7

  解析

• 3．已知向量

  a

  =

  （

  3

  ，

  1

  ）

  ，

  b

  =

  （

  0

  ，-

  1

  ）

  ，

  c

  =

  （

  k

  ,

  3

  ）

  ．若

  a

  -

  2

  b

  与

  c

  共线，则k=（　　）

  A．1

  B．3

  C． 1 2

  D． 3 2
  组卷：210引用：2难度：0.8

  解析

• 4．已知α为第二象限角，sinα+cosα=

  3

  3

  ，则cos2α=（　　）

  A．- 5 3

  B．- 5 9

  C． 5 9

  D． 5 3
  组卷：5576引用：87难度：0.7

  解析

• 5．对于不重合的两个平面α与β，给定下列条件：
  ①存在平面γ，使得α，β都垂直于γ；
  ②存在平面γ，使得α，β都平行于γ；
  ③存在直线l⊂α，直线m⊂β，使得l∥m；
  ④存在异面直线l、m,使得l∥α，l∥β，m∥α，m∥β．
  其中，可以判定α与β平行的条件有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：213引用：5难度：0.9

  解析

• 6．若将函数f（x）=sin2x+cos2x的图象向右平移φ个单位，所得图象关于y轴对称，则φ的最小正值是（　　）

  A． π 8

  B． π 4

  C． 3 π 8

  D． 3 π 4
  组卷：3794引用：88难度：0.7

  解析

三、解答题共5小题，共55分.解答应写出文字说明、演算步骤或证明过程.

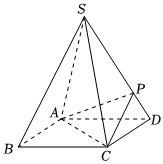• 19．如图，正四棱锥S-ABCD，SA=SB=SC=SD=4，

  AB

  =

  2

  2

  ，P为侧棱SD上的点，且SP=3PD．
  （1）求正四棱锥S-ABCD的表面积；
  （2）求点S到平面PAC的距离；
  （3）侧棱SC上是否存在一点E，使得BE∥平面PAC．若存在，求

  SE

  EC

  的值；若不存在，试说明理由．
  组卷：234引用：3难度：0.5

  解析

• 20．已知有穷数列

  A

  ：

  a

  1

  ，

  a

  2

  ，

  ⋯

  ，

  a

  N

  （

  N

  ∈

  N

  *

  ，

  N

  ≥

  3

  ）

  满足a_i∈{-1，0，1}（i=1，2，⋯，N）．给定正整数m,若存在正整数s,t（s≠t），使得对任意的k∈{0，1，2，⋯，m-1}，都有a_s+k=a_t+k，则称数列A是m-连续等项数列．
  （1）判断数列A：1，-1，0，-1，0，-1，1是否是3-连续等项数列，并说明理由；
  （2）若项数为N的任意数列A都是2-连续等项数列，求N的最小值；
  （3）若数列A：a₁，a₂，⋯，a_N不是4-连续等项数列，而数列A₁：a₁，a₂，⋯，a_N，-1，数列A₂：a₁，a₂，⋯，a_N，0与数列A₃：a₁，a₂，⋯，a_N，1都是4-连续等项数列，且a₃=0，求a_N的值．
  组卷：176引用：4难度：0.1

  解析