当前位置：试卷中心 > 试卷详情

2022-2023学年河北省邯郸市部分学校八年级（上）期中数学试卷

发布：2024/7/3 8:0:9

一、选择题（本大题共16个小题.1～10小题每题3分，11～16小题每题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1．钢架雪车是2022年北京冬奥会的比赛项目之一．下面这些钢架雪车运动标志是轴对称图形的是（　　）
A． B． C． D．
组卷：184引用：13难度：0.9
解析
2．在平面直角坐标系中，点A（1，-4）关于x轴对称的点的坐标为（　　）
A．（1，4） B．（-1，4） C．（0，-4） D．（-1，-4）
组卷：24引用：4难度：0.7
解析
3．下列正多边形中，内角和为540°的是（　　）
A． B． C． D．
组卷：398引用：9难度：0.8
解析
4．如图，用纸板挡住部分三角形后，能用尺规画出与此三角形全等的三角形，其全等的依据是（　　）
A．ASA B．AAS C．SAS D．HL
组卷：99引用：8难度：0.8
解析
5．如图，若α为正六边形的外角，则α的度数为（　　）
A．60° B．45° C．72° D．50°
组卷：186引用：4难度：0.8
解析
6．如图，△ABF≌△ACE，点B和点C是对应顶点，则下列结论中不一定成立的是（　　）
A．∠B=∠C B．BE=CF C．∠BAE=∠CAF D．AE=EF
组卷：47引用：4难度：0.5
解析
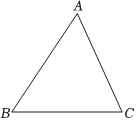7．如图，物业公司计划在小区内修建一个电动车充电桩，要求到A，B，C三个出口的距离都相等，则充电桩应建在（　　）
A．△ABC的三条高的交点处
B．△ABC的三条角平分线的交点处
C．△ABC的三条中线的交点处
D．△ABC的三条边的垂直平分线的交点处
组卷：104引用：4难度：0.5
解析
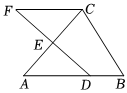8．如图，E是△ABC的边AC的中点，CF∥AB，连接FE并延长交AB于点D，若AB=9，CF=6，则BD的长为（　　）
A．1.5 B．2 C．3 D．3.5
组卷：140引用：5难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共7个小题，共69分.解答应写出文字说明、证明过程或演算步骤）

25．如图，AE=AF，AE⊥AF，点E，F，B在同一直线上，AB=AC，∠BAC=90°．
（1）判断△AEB与△AFC是否全等？若全等，请给出证明；若不全等，请说明理由；
（2）当EF和BF满足什么数量关系时，CE=CB？请给出结论并说明理由．
组卷：32引用：4难度：0.5
解析
26．【问题提出】如图1，△ABC是直角三角形，∠BAC=90°，AB=AC，直线l经过点A，分别过点B，C向直线l作垂线，垂足分别为D，E．求证：△ABD≌△CAE；
【变式探究】若图1中的点B，C在直线l的两侧，其他条件不变（如图2所示），判断△ABD与△CAE是否依然全等，并说明理由；
【深入思考】如图3，在△ABC中，AB=AC，直线l经过点A，且点B，C位于直线l的两侧，若∠BDA+∠BAC=180°，∠BDA=∠AEC，判断线段BD，CE，DE之间的数量关系，并加以说明．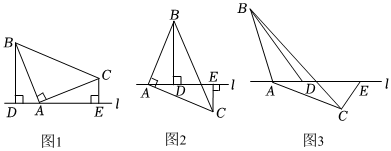
组卷：118引用：4难度：0.2
解析