当前位置：试卷中心 > 试卷详情

2023-2024学年湖北省武汉一初慧泉中学九年级（上）月考数学试卷（9月份）

发布：2024/8/27 9:0:9

一、选择题（共10小题，每小题3分，共30分）

1．将一元二次方程5x²-1=4x化成一般形式后，二次项的系数和一次项系数分别是（　　）
A．5，-1 B．5，4 C．5，-4 D．5，1
组卷：1540引用：39难度：0.9
解析
2．下列四张扑克牌的牌面，不是中心对称图形的是（　　）
A． B． C． D．
组卷：281引用：47难度：0.9
解析
3．将一元二次方程x²-2x-3=0配方后所得的方程是（　　）
A．（x-2）²=4 B．（x-1）²=4 C．（x-1）²=3 D．（x-2）²=3
组卷：108引用：7难度：0.9
解析
4．已知一元二次方程x²+4x-1=0的两根分别为m,n,则mn的值是（　　）
A．-4 B．1 C．4 D．-1
组卷：85引用：2难度：0.7
解析
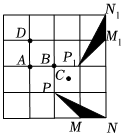5．在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M₁N₁P₁，则其旋转中心可能是（　　）
A．点A B．点B C．点C D．点D
组卷：3256引用：139难度：0.9
解析
6．若二次函数y=ax²+bx+c的部分图象如图所示，则方程ax²+bx+c=0的解是（　　）
A．x=1 B．x=1或-4
C．x₁=1，x₂=-3 D．x₁=-1，x₂=-2
组卷：798引用：11难度：0.7
解析
7．将抛物线y=2x²-1的图象先向右平移3个单位，再向上平移4个单位，得到的抛物线的解析式是（　　）
A．y=2（x+3）²+4 B．y=2（x-3）²+4
C．y=（x-3）²+3 D．y=2（x-3）²+3
组卷：599引用：8难度：0.7
解析
8．李师傅去年开了一家商店，今年1月份开始盈利，2月份盈利2000元，4月份的盈利达到2880元，且从2月到4月，若每月盈利的平均增长率都相同．那么按照这个平均增长率，预计五月份这家商店的盈利将达到（　　）元．
A．3320 B．3440 C．3450 D．3456
组卷：336引用：5难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共8小题，共72分）

23．提出问题：
如图1，在△ABC和△DEC中，∠ACB=∠DCE=120°，BC=AC，EC=DC，点E在△ABC内部，直线AD与BE交于点F，线段AF、BF、CF之间存在怎样的数量关系？
探究问题：
（1）先将问题特殊化，如图2，当点D、F重合时，直接写出一个等式，表示线段AF、BF、CF之间的数量关系；
（2）再探究一般情形，如图1，当点D、F不重合时，证明（1）中的结论仍然成立．
解决问题：
（3）如图3，在△ABC中，∠C=90°，AC=BC．若∠ADC=135°，记AD=a,BD=b,CD=c,补充并探究图形，直接写出a、b、c之间的数量关系．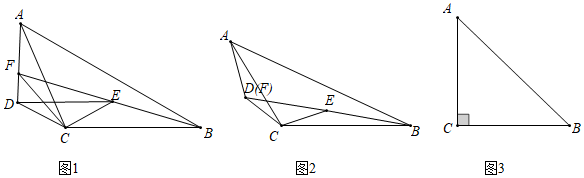
组卷：517引用：2难度：0.1
解析
24．已知抛物线y=-x²+bx+c（bc≠0）的顶点为D，与x轴交于A，B两点（A在B左边）．
（1）若该抛物线的顶点D坐标为（1，4），求其解析式；
（2）如图（1），在（1）的条件下，P，Q为y轴上的两个关于原点对称的动点，射线BP，BQ分别与抛物线交于M，N两点，求
MN
PQ
的值．
（3）如图（2），已知抛物线的顶点D在直线l：y=-x+3上滑动，且与直线l交于另一点E，若△ADE的面积为
15
8
，求抛物线顶点D的坐标．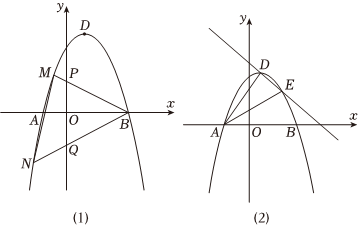
组卷：193引用：1难度：0.4
解析