2022-2023学年浙江省衢温5+1联盟高二（上）期中数学试卷

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={x|x+2≥0}，B={x|（x-2）（x+3）＜0}，则A∩B=（　　）

  A．[-2，2）

  B．（-3，2）

  C．[-2，+∞）

  D．（-3，-2]
  组卷：5引用：2难度：0.7

  解析

• 2．复数

  3

  -

  i

  1

  -

  2

  i

  在复平面内对应的点所在的象限为（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：13引用：5难度：0.7

  解析

• 3．已知圆C₁：（x-2m）²+（y-2m）²=9（m-2）与圆C₂：x²+y²-8x-8y+34-m=0，则“m=4”是“圆C₁与圆C₂外切”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：63引用：5难度：0.6

  解析

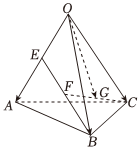• 4．如图，四面体OABC中，点E为OA中点，F为BE中点，G为CF中点，设

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，若

  OG

  可用

  a

  ，

  b

  ，

  c

  表示为（　　）

  A． 1 4 a + 1 4 b + 1 2 c	B． 1 8 a + 1 4 b + 1 2 c
  C． 1 8 a + 1 4 b + 1 4 c	D． 1 8 a + 1 8 b + 1 2 c
  组卷：129引用：6难度：0.5

  解析

• 5．设a=log₇2，b=log₈3，

  c

  =

  1

  2

  ，则（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．a＜c＜b

  D．c＜b＜a
  组卷：28引用：2难度：0.7

  解析

• 6．已知圆锥底面半径为1，母线长为2，则该圆锥的外接球的表面积为（　　）

  A． 8 3 π

  B． 16 3 π

  C．8π

  D．16π
  组卷：37引用：2难度：0.7

  解析

• 7．超市举行回馈顾客有奖促销活动，顾客购买一定金额商品后可参加抽奖活动，抽奖原则是：从装有4个红球、6个黄球的甲箱和装有5个红球、5个黄球的乙箱中，各随机摸出一个球，在摸出的2个球中，若都是红球，则获一等奖，得奖金20元；若只有1个红球，则获二等奖，得奖金10元；若没有红球，则不获奖．现某顾客有3次摸奖机会，则该顾客3次摸奖共获得40元奖励的概率为（　　）

  A． 93 500

  B． 3 20

  C． 31 500

  D． 9 250
  组卷：17引用：1难度：0.7

  解析

四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．如图1，等腰梯形AECD是由三个全等的等边三角形拼成，现将△BCE沿BC翻折至△BCP，使得PD=

  3

  2

  AB，如图2所示．
  
  （1）求证：PD⊥BC；
  （2）在直线PD上是否存在点M，使得直线BM与平面APD所成角的余弦值为

  10

  4

  ？若存在，求出

  PM

  DM

  的值；若不存在，说明理由．
  组卷：35引用：1难度：0.4

  解析

• 22．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

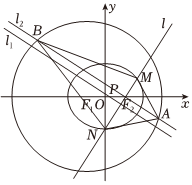  =1（a＞b＞0）的离心率为

  1

  2

  ，其左、右焦点为F₁、F₂，过F₂作不与x轴重合的直线l交椭圆C于M、N两点，△F₁MN的周长为8．
  （1）求椭圆C的方程；
  （2）设线段MN的垂直平分线l₁交x轴于点P，是否存在实数λ，使得|MN|=λ|PF₂|？若存在，求出λ的值；若不存在，请说明理由；
  （3）以F₁为圆心4为半径作圆，过F₂作直线l₁∥l₂交圆F于A、B两点，求四边形AMBN的面积的最小值及取得最小值时直线l的方程．
  组卷：21引用：1难度：0.6

  解析