2022-2023学年河北省唐山市冀东名校高二(下)期末数学试卷
发布:2024/6/10 8:0:9
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1.设集合A={x|x<3x-1},B={x|-1<x<3},则A∪B=( )
组卷:429引用:6难度:0.8 -
2.若复数z满足(1+i)z=4-2i(i为虚数单位),则z的共轭复数
=( )z组卷:23引用:3难度:0.8 -
3.已知幂函数
,下列能成为“f(x)是R上奇函数”充分条件的是( )f(x)=xmn(m,n∈Z)组卷:171引用:9难度:0.7 -
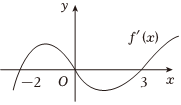 4.已知函数f(x)导函数f'(x)的图象如图所示,则( )组卷:125引用:6难度:0.8
4.已知函数f(x)导函数f'(x)的图象如图所示,则( )组卷:125引用:6难度:0.8 -
5.已知函数f(x)=ex+e-x+lg|x|,则不等式f(x+1)>f(2x-1)的解集为( )
组卷:514引用:5难度:0.5 -
6.已知函数f(x)=x+
,g(x)=2x+a,若∀x1∈[4x,1],∃x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是( )12组卷:924引用:16难度:0.7 -
7.三个数
的大小顺序为( )a=2e2,b=ln2,c=ln33组卷:370引用:9难度:0.7
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.下表是某农村居民2018年至2022年家庭人均收入(单位:万元).
(1)利用相关系数r判断y与x的相关关系的强弱(当0.75<|r|≤1时,y与x的相关关系较强,否则相关关系较弱,精确到0.01); (2)求y关于x的线性回归方程年份 2018 2019 2020 2021 2022 年份代码x 1 2 3 4 5 家庭人均收入y(万元) 1.2 1.4 1.5 1.6 1.8 ,并预测2023年该农村居民的家庭人均收入.附:对于一组数据(x1,y1)、(x2,y2)、…、(xn,yn),其回归直线̂y=̂bx+̂a的斜率和截距的最小二乘估计分别为̂y=̂bx+̂a,̂b=n∑i=1xi•yi-n•x•yn∑i=1x2i-n•x2,样本相关系数r=̂a=y-̂bx.参考数据:n∑i=1xi•yi-n•x•yn∑i=1(xi-x)2•n∑i=1(yi-y)2≈1.414.2组卷:45引用:5难度:0.5 -
22.已知函数f(x)=ex-ax-1.
(1)讨论函数f(x)的单调性;
(2)若f(x)有且仅有2个零点,求实数a的取值范围.组卷:52引用:3难度:0.5


