2023-2024学年广东省东莞市东华初级中学八年级（上）月考数学试卷（10月份）

一、选择题（共10小题，每小题3分，共30分）

• 1．一个三角形的两条边分别为3cm,7cm,则它的第三边可能是（　　）

  A．3cm

  B．7cm

  C．10cm

  D．12cm
  组卷：290引用：9难度：0.7

  解析

• 2．下列四个图形中，线段BE是△ABC的高的是（　　）

  A．	B．
  C．	D．
  组卷：2836引用：52难度：0.6

  解析

• 3．下列生活实物中，没有应用到三角形的稳定性的是（　　）

  A． 太阳能热水器	B． 篮球架
  C． 三脚架	D． 活动衣架
  组卷：647引用：26难度：0.7

  解析

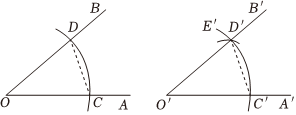• 4．用直尺和圆规作一个角等于已知角的示意图如下，则要说明∠AOB=∠A′O′B′，需要证明△COD和△C'O'D'，则这两个三角形全等的依据是（　　）

  A．SAS

  B．AAS

  C．SSS

  D．ASA
  组卷：237引用：10难度：0.5

  解析

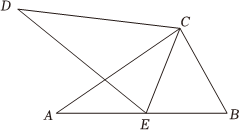• 5．如图，△ABC≌△DEC，∠ACB=80°，∠ACE=30°，则∠DCA的度数为（　　）

  A．30°

  B．40°

  C．50°

  D．60°
  组卷：37引用：3难度：0.5

  解析

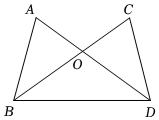• 6．如图，AD，BC相交于点O，∠A=∠C，要根据“ASA”证明△AOB≌△COD，还需添加的一个条件是（　　）

  A．AB=CD

  B．AO=CO

  C．BO=DO

  D．∠ABO=∠CDO
  组卷：216引用：4难度：0.7

  解析

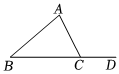• 7．如图，点D是△ABC边BC延长线上的一点，∠A=75°，∠ACD=105°，则∠B=（　　）

  A．30°

  B．35°

  C．40°

  D．45°
  组卷：934引用：10难度：0.9

  解析

五、解答题（三）（本大题2小题，每小题12分，共24分）

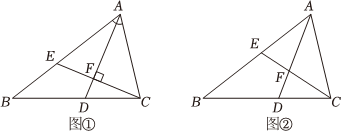• 22．在△ABC中，∠BAC=60°，∠ACB=2∠B，AD平分∠BAC交BC于点D，
  （1）求∠B的度数；
  （2）如图①，若CE⊥AD于点F，交AB于点E．求∠ECD的度数．
  （3）如图②，若CE平分∠ACB交AB于点E，交AD于点F，求∠AFC的度数．
  组卷：392引用：4难度：0.5

  解析

• 23．[课本习题]如图①，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D、E．
  求证：BE=CD；
  [改编]在图①中的边AD上取一点F，使DF=CD，连接BF交DE于点G，连接AG（如图②）．
  （1）求证：△FDG≌△BEG；
  （2）若AD=5，BE=2，请直接写出△AFG的面积．
  组卷：150引用：2难度：0.5

  解析