2022-2023学年湖南省长沙市长沙县高一(下)期末数学试卷
发布:2024/6/15 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知i是虚数单位,复数
,则z是( )z=-1+ii组卷:61引用:2难度:0.8 -
2.已知一个圆锥的母线长为2,其侧面积为2π,则该圆锥的体积为( )
组卷:330引用:6难度:0.8 -
3.为庆祝中国共产党成立100周年,某市举办“红歌大传唱”主题活动,以传承红色革命精神,践行社会主义路线,某高中有高一、高二、高三分别600人、500人、700人,欲采用分层抽样法组建一个18人的高一、高二、高三的红歌传唱队,则应抽取高三( )
组卷:298引用:6难度:0.7 -
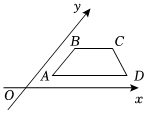 4.用斜二测画法画出的某平面图形的直观图如图所示,边AB平行于y轴,BC,AD平行于x轴,已知四边形的面积为6cm2,则原四边形的面积为( )cm2.组卷:345引用:4难度:0.7
4.用斜二测画法画出的某平面图形的直观图如图所示,边AB平行于y轴,BC,AD平行于x轴,已知四边形的面积为6cm2,则原四边形的面积为( )cm2.组卷:345引用:4难度:0.7 -
5.△ABC中,a=6,
,A=30°,则边c等于( )b=63组卷:114引用:4难度:0.9 -
6.要得到函数
的图象,只需( )y=3sin(2x+π5)组卷:776引用:8难度:0.7 -
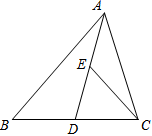 7.如图,△ABC中,=AB,a=AC,D为BC中点,E为AD中点,b用CE和a表示为b=CEλa,则+μb=( )λμ组卷:479引用:5难度:0.6
7.如图,△ABC中,=AB,a=AC,D为BC中点,E为AD中点,b用CE和a表示为b=CEλa,则+μb=( )λμ组卷:479引用:5难度:0.6
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
-
21.记△ABC的内角A,B,C的对边分别为a,b,c,且
.3c=3acosB-asinB
(1)求A的大小;
(2)若A的角平分线交BC于D,且AD=3,求△ABC面积的最小值.组卷:396引用:11难度:0.5 -
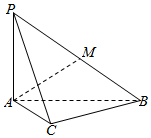 22.如图,三棱锥P-ABC中,∠ACB=90°,PA⊥底面ABC.
22.如图,三棱锥P-ABC中,∠ACB=90°,PA⊥底面ABC.
(Ⅰ)求证:平面PAC⊥平面PBC;
(Ⅱ)若AC=BC=PA,M是PB的中点,求AM与平面PBC所成角的正切值.组卷:988引用:17难度:0.3


