2023-2024学年山东省济南市市中区育英中学九年级(上)月考数学试卷(10月份)
发布:2024/9/8 12:0:8
一.选择题(共12小题,每题3分)
-
1.已知cosα=
,且α是锐角,则α=( )32组卷:1026引用:7难度:0.7 -
2.若
,则xx-y=12的值为( )xy组卷:463引用:7难度:0.9 -
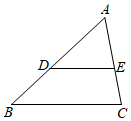 3.如图,在△ABC中,DE∥BC,若AD:DB=3:2,DE=6cm,则BC的长为( )组卷:339引用:4难度:0.6
3.如图,在△ABC中,DE∥BC,若AD:DB=3:2,DE=6cm,则BC的长为( )组卷:339引用:4难度:0.6 -
4.已知点A(-4,y1),B(-2,y2),C(3,y3)都在反比例函数y=
(k<0)的图象上,则y1,y2,y3的大小关系为( )kx组卷:3952引用:38难度:0.8 -
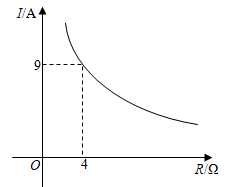 5.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )组卷:2582引用:27难度:0.6
5.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )组卷:2582引用:27难度:0.6 -
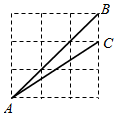 6.如图,A,B,C是正方形网格的格点,连接AC,AB,则tan∠BAC的值是( )组卷:1267引用:5难度:0.6
6.如图,A,B,C是正方形网格的格点,连接AC,AB,则tan∠BAC的值是( )组卷:1267引用:5难度:0.6 -
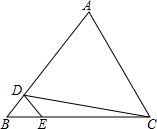 7.如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=( )组卷:4828引用:84难度:0.7
7.如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=( )组卷:4828引用:84难度:0.7 -
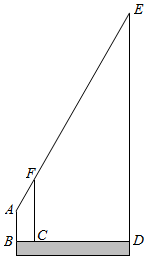 8.如图,某测量工作人员站在地面点B处利用标杆FC测量一旗杆ED的高度.测量人员眼睛处点A与标杆顶端处点F,旗杆顶端处点E在同一直线上,点B,C,D也在同一条直线上.已知此人眼睛到地面距离AB=1.6米,标杆高FC=3.2米,且BC=1米,CD=5米,则旗杆的高度为( )组卷:1309引用:9难度:0.5
8.如图,某测量工作人员站在地面点B处利用标杆FC测量一旗杆ED的高度.测量人员眼睛处点A与标杆顶端处点F,旗杆顶端处点E在同一直线上,点B,C,D也在同一条直线上.已知此人眼睛到地面距离AB=1.6米,标杆高FC=3.2米,且BC=1米,CD=5米,则旗杆的高度为( )组卷:1309引用:9难度:0.5
三.解答题
-
23.在△ABC和△ADE中,BA=BC,DA=DE.且∠ABC=∠ADE=α,点E在△ABC的内部,连接EC,EB和BD,并且∠ACE+∠ABE=90°.
(1)如图①,当α=60°时,线段BD与CE的数量关系为,线段EA,EB,EC的数量关系为;
(2)如图②,当α=90°时,请写出线段EA,EB,EC的数量关系,并说明理由;
(3)在(2)的条件下,当点E在线段CD上时,若BC=2,请直接写出△BDE的面积.5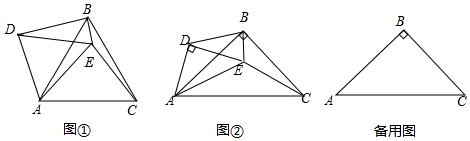 组卷:3097引用:3难度:0.1
组卷:3097引用:3难度:0.1 -
24.阅读理解题:阅读材料:
如图1,四边形ABCD是矩形,△AEF是等腰直角三角形,记∠BAE为α、∠FAD为β,若tanα=,则tanβ=12.13
证明:设BE=k,
∵tanα=,12
∴AB=2k,
易证△AEB≌△EFC(AAS).
∴EC=2k,CF=k,
∴FD=k,AD=3k,
∴tanβ==DFAD=k3k,13
若α+β=45°时,当tanα=,则tanβ=12.13
同理:若α+β=45°时,当tanα=,则tanβ=13.12
根据上述材料,完成下列问题:
如图2,直线y=3x-9与反比例函数y=(x>0)的图象交于点A,与x轴交于点B.将直线AB绕点A顺时针旋转45°后的直线与y轴交于点E,过点A作AM⊥x轴于点M,过点A作AN⊥y轴于点N,已知OA=5.mx
(1)求反比例函数的解析式;
(2)直接写出tan∠BAM、tan∠NAE的值;
(3)求直线AE的解析式.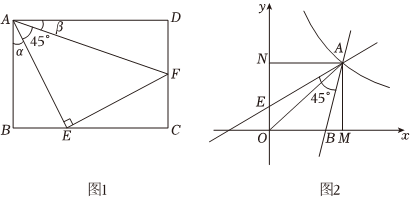 组卷:1647引用:4难度:0.3
组卷:1647引用:4难度:0.3


