2022-2023学年云南省临沧市凤庆一中高二(下)期中数学试卷
发布:2024/5/18 8:0:8
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1.若
,则f'(-2)=( )limΔx→0f(-2+Δx)-f(-2-Δx)Δx=-2组卷:200引用:5难度:0.8 -
2.已知某地区中小学生人数如图①所示,为了解该地区中小学生的近视情况,卫生部门根据当地中小学生人数,用分层抽样的方法抽取了10%的学生进行调查,调查数据如图②所示,则估计该地区中小学生的平均近视率为( )
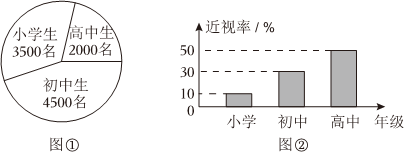 组卷:46引用:7难度:0.7
组卷:46引用:7难度:0.7 -
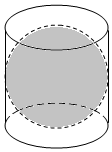 3.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现,即:圆柱的体积与其内切球的体积比为定值.现在让我们来重温这个伟大发现.圆柱的体积与球的体积之比为( )组卷:109引用:3难度:0.7
3.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现,即:圆柱的体积与其内切球的体积比为定值.现在让我们来重温这个伟大发现.圆柱的体积与球的体积之比为( )组卷:109引用:3难度:0.7 -
4.已知
,则cos(α+π6)=-210=( )sin(2α-π6)组卷:291引用:4难度:0.7 -
5.函数f(x)在x=x0处的导数
( )f′(x0)=limΔx→0f(x0+Δx)-f(x0)Δx组卷:12引用:1难度:0.8 -
6.已知双曲线
,其中a2,b2,c2成等差数列,则该双曲线的渐近线方程为( )Γ:y2a2-x2b2=1(a>0,b>0)组卷:84引用:2难度:0.6 -
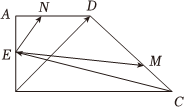 7.如图所示,梯形ABCD中,AD∥BC,点E为AB的中点,,若向量BA•BC=0,BD•BA=BD•AD=4在向量CE上的投影向量的模为4,设M、N分别为线段CD、AD上的动点,且CB,则CM=λCD,AN=19λAD的最大值是( )EM•EN组卷:50引用:1难度:0.5
7.如图所示,梯形ABCD中,AD∥BC,点E为AB的中点,,若向量BA•BC=0,BD•BA=BD•AD=4在向量CE上的投影向量的模为4,设M、N分别为线段CD、AD上的动点,且CB,则CM=λCD,AN=19λAD的最大值是( )EM•EN组卷:50引用:1难度:0.5
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
-
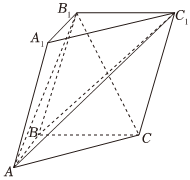 21.如图,三棱柱ABC-A1B1C1中,AA1⊥A1B1,AB⊥BC,侧面BCC1B1为菱形.
21.如图,三棱柱ABC-A1B1C1中,AA1⊥A1B1,AB⊥BC,侧面BCC1B1为菱形.
(1)求证:平面ABC1⊥平面AB1C;
(2)若BC=2AB=2,∠B1BC=60°,求二面角B1-AC1-B的余弦值组卷:39引用:1难度:0.5 -
22.设椭圆C:
=1(a>b>0)的左、右焦点分别为F1、F2,离心率e=x2a2+y2b2,长轴为4,且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.12
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若=-2,其中O为坐标原点,求直线l的斜率;OM•ON
(Ⅲ)若AB是椭圆C经过原点O的弦,且MN∥AB,判断是否为定值?若是定值,请求出,若不是定值,请说明理由.|AB|2|MN|组卷:773引用:4难度:0.6


