2022-2023学年浙江省绍兴市嵊州市剡城中学教育集团八年级（上）期中数学试卷

一、选择题：本大题共10个小题，每小题2分，共20分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．下列图形中为轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：55引用：2难度：0.9

  解析

• 2．如图，工人师傅砌门时，为使长方形门框ABCD不变形，常用木条EF将其固定，这种做法的依据是（　　）

  A．两点之间线段最短	B．长方形的对称性
  C．四边形具有不稳定性	D．三角形具有稳定性
  组卷：834引用：9难度：0.7

  解析

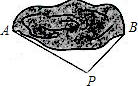• 3．为估计池塘两岸A、B间的距离，杨阳在池塘一侧选取了一点P，测得PA=16m,PB=12m,那么AB间的距离不可能是（　　）

  A．5m

  B．15m

  C．20m

  D．28m
  组卷：679引用：51难度：0.9

  解析

• 4．对假命题“若a＞b,则a²＞b²”举反例，正确的反例是（　　）

  A．a=-1，b=0

  B．a=2，b=-1

  C．a=-1，b=-2

  D．a=-1，b=2
  组卷：352引用：11难度：0.7

  解析

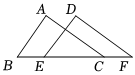• 5．如图，BE=CF，AB=DE，添加下列哪一个条件可以推证△ABC≌△DEF（　　）

  A．BC=EF

  B．∠A=∠D

  C．AC∥DF

  D．∠B=∠DEF
  组卷：663引用：13难度：0.6

  解析

• 6．由下列条件不能判断△ABC是直角三角形的是（　　）

  A．∠A：∠B：∠C=3：4：5	B．AB：BC：AC=3：4：5
  C．∠A+∠B=∠C	D．AB2=BC2+AC2
  组卷：1548引用：39难度：0.8

  解析

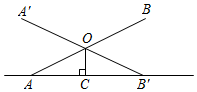• 7．同学们都玩过跷跷板的游戏，如图是一个跷跷板的示意图，立柱OC与地面垂直，OA=OB．当跷跷板的一头A着地时，∠AOA′=50°，则当跷跷板的另一头B着地时，∠COB′等于（　　）

  A．25°

  B．50°

  C．65°

  D．130°
  组卷：189引用：4难度：0.7

  解析

• 8．已知等腰三角形的一边长为5，另一边长为10，则这个等腰三角形的周长为（　　）

  A．25

  B．25或20

  C．20

  D．15
  组卷：908引用：18难度：0.9

  解析

三、解答题：共50分.解答应写出文字说明、证明过程或演算步骤.

• 25．【初步探索】
  （1）如图1：在四边形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且EF=BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．
  小王同学探究此问题的方法是：延长FD到点G，使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是

  ．
  【灵活运用】
  （2）如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且EF=BE+FD，上述结论是否仍然成立，并说明理由．
  【拓展延伸】
  （3）已知在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF=BE+FD，请直接写出∠EAF与∠DAB的数量关系．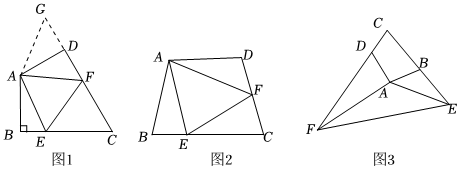
  
  组卷：2427引用：21难度：0.1

  解析

• 26．如图，△ABC中，BA=BC，CO⊥AB于点O，AO=4，BO=6．
  （1）求BC，AC的长；
  （2）若点D是射线OB上的一个动点，作DE⊥AC于点E，连结OE．
  ①当点D在线段OB上时，若△AOE是以AO为腰的等腰三角形，请求出所有符合条件的OD的长．
  ②设DE交直线BC于点F，连结OF，若S_△OBF：S_△OCF=1：4，则BD的长为

  （直接写出所有结果）．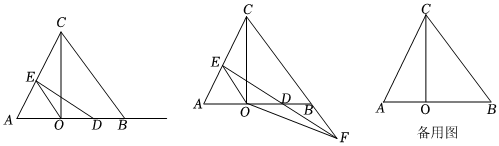
  
  组卷：773引用：3难度：0.3

  解析