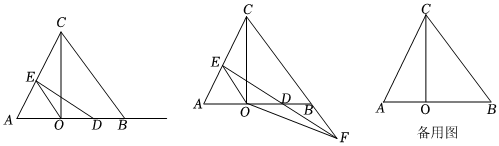
如图，△ABC中，BA=BC，CO⊥AB于点O，AO=4，BO=6．
（1）求BC，AC的长；
（2）若点D是射线OB上的一个动点，作DE⊥AC于点E，连结OE．
①当点D在线段OB上时，若△AOE是以AO为腰的等腰三角形，请求出所有符合条件的OD的长．
②设DE交直线BC于点F，连结OF，若S△OBF：S△OCF=1：4，则BD的长为 103或2103或2（直接写出所有结果）．
10
3
10
3
【考点】勾股定理；等腰三角形的判定与性质．
【答案】或2
10
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/27 12:0:9组卷：773引用：3难度：0.3
相似题
-
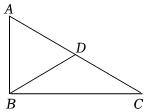1．如图所示，在Rt△ABC中，∠B=90°，BC=12，AB=5，则斜边上的中线BD长是（ ）发布：2025/6/8 6:30:2组卷：7引用：1难度：0.6 -
2．在△ABC中，∠ACB=90°，点D是AB边上的中点，若BC=6，AC=8，则CD的长为（ ）
发布：2025/6/8 6:30:2组卷：12引用：2难度：0.6 -
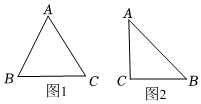3．如果三角形有一边上的中线恰好等于这边的长，那么我们称这个三角形为“美丽三角形”．（注：直角三角形斜边上的中线等于斜边的一半）
（1）如图1，在△ABC中，AB=AC=，BC=4，求证：△ABC是“美丽三角形”；25
（2）如图2，在Rt△ABC中，∠C=90°，AC=4，若Rt△ABC是“美丽三角形”，求BC的长．3发布：2025/6/8 6:30:2组卷：158引用：3难度：0.4
