2023-2024学年江苏省盐城市滨海县滨淮初中教育集团九年级(上)第一次学情研判数学试卷
发布:2024/9/4 15:0:9
一、选择题(本题共8小题,每小题3分,本题共24分)
-
1.下列方程是一元二次方程的是( )
组卷:36引用:1难度:0.5 -
2.用配方法将方程x2-4x-1=0变形为(x-2)2=m,则m的值是( )
组卷:1174引用:23难度:0.6 -
3.已知⊙O的半径为10cm,点P到圆心O的距离为8cm,则点P和圆的位置关系( )
组卷:203引用:4难度:0.8 -
4.下列说法:(1)三个点确定一个圆;(2)相等的圆心角所对的弦相等;(3)同弧或等弧所对的圆周角相等;(4)三角形的外心到三角形三条边的距离相等;(5)外心在三角形的一边上的三角形是直角三角形;其中正确的有( )
组卷:102引用:3难度:0.5 -
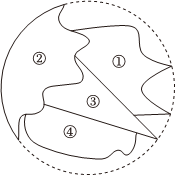 5.一圆形玻璃被打碎后,其中四块碎片如图所示,若选择其中一块碎片带到商店,配制与原来大小一样的圆形玻璃,选择的是( )组卷:299引用:4难度:0.9
5.一圆形玻璃被打碎后,其中四块碎片如图所示,若选择其中一块碎片带到商店,配制与原来大小一样的圆形玻璃,选择的是( )组卷:299引用:4难度:0.9 -
6.有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程中符合题意的是( )
组卷:2356引用:39难度:0.6 -
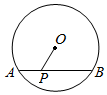 7.如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点,则线段OP长的最小值是( )组卷:1150引用:8难度:0.6
7.如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点,则线段OP长的最小值是( )组卷:1150引用:8难度:0.6 -
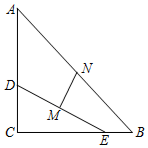 8.如图,△ABC中,∠C=90°,AC=10,BC=8,线段DE的两个端点D、E分别在边AC,BC上滑动,且DE=6,若点M、N分别是DE、AB的中点,则MN的最小值为( )组卷:2620引用:8难度:0.5
8.如图,△ABC中,∠C=90°,AC=10,BC=8,线段DE的两个端点D、E分别在边AC,BC上滑动,且DE=6,若点M、N分别是DE、AB的中点,则MN的最小值为( )组卷:2620引用:8难度:0.5
二、填空题(本题共有10小题,每题3分,本题共30分)
-
9.当m=时,x2-2(m-3)x+9是完全平方式.
组卷:813引用:4难度:0.8
三、解答题(共96分)
-
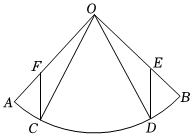 26.如图,在扇形AOB中,点C、D在上,ˆAB,点F、E分别在半径OA、OB上,OF=OE,联结DE、CF.ˆAD=ˆCB
26.如图,在扇形AOB中,点C、D在上,ˆAB,点F、E分别在半径OA、OB上,OF=OE,联结DE、CF.ˆAD=ˆCB
(1)求证:DE=CF;
(2)设点P为的中点,联结CD、EF、PO,线段PO交CD于点M、交EF于点N.如果PO∥DE,求证:四边形MNED是矩形.ˆCD组卷:868引用:4难度:0.6 -
27.几何模型
条件:如图1,A、B是直线l同侧的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点B关于直线l的对称点B’,连接AB’交l于点P,则PA+PB=AB’的值最小(不必证明).
直接应用
如图2,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为.
变式练习
如图3,点A是半圆上(半径为1)的三等分点,B是()的中点,P是直径MN上一动点,求PA+PB的最小值.ˆAN
深化拓展
(1)如图4,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,求BM+MN的最小值.2
(2)如图5,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.
(要求:保留作图痕迹,并简述作法.)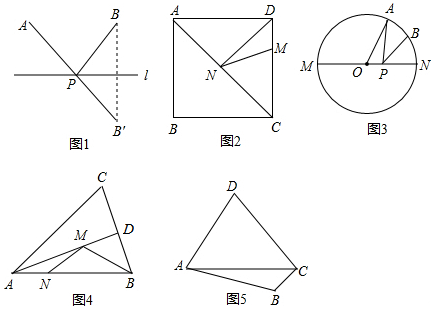 组卷:1290引用:5难度:0.5
组卷:1290引用:5难度:0.5


