2023-2024学年北京市海淀区八一学校高三（上）开学数学试卷

一、选择题共10小题，每小题4分，共40分.在每题列出的四个选项中，选出符合题目要求的一项.

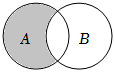• 1．若集合A={1，2，3，4，5}，集合B={x|x（4-x）＜0}，则图中阴影部分表示（　　）

  A．{1，2，3，4}

  B．{1，2，3}

  C．{4，5}

  D．{1，4}
  组卷：186引用：11难度：0.9

  解析

• 2．设z=1+i,则z²-i=（　　）

  A．i

  B．-i

  C．1

  D．-1
  组卷：167引用：6难度：0.8

  解析

• 3．下列函数中，值域为（1，+∞）的是（　　）

  A．y=2x+1

  B． y = 1 x + 1

  C．y=log2|x|

  D．y=x2+1
  组卷：425引用：4难度：0.9

  解析

• 4．“m＞2”是“方程

  x

  2

  2

  -

  m

  +

  y

  2

  m

  +

  1

  =

  1

  表示双曲线”的（　　）条件．

  A．必要不充分条件	B．充分不必要条件
  C．充要条件	D．既不充分也不必要条件
  组卷：143引用：5难度：0.7

  解析

• 5．埃及胡夫金字塔是世界古代建筑奇迹之一，它的形状可视为一个正四棱锥，其侧面与底面所成角的余弦值为

  5

  -

  1

  2

  ，则侧面三角形的顶角的正切值为（　　）

  A．2

  B．3

  C． 5 - 1 2

  D． 5 + 1 2
  组卷：349引用：5难度：0.6

  解析

• 6．直线l经过点A（0，b），且与直线y=2x平行，如果直线l与曲线y=x²相切，那么b等于（　　）

  A． - 1 4

  B．-1

  C．1

  D． 1 2
  组卷：62引用：1难度：0.6

  解析

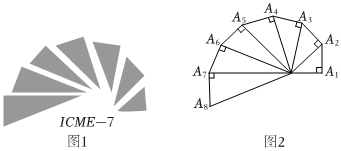• 7．图1是第七届国际数学教育大会的会徽图案，会徽的主体图案是由如图2所示的一连串直角三角形演化而成的，其中OA₁=A₁A₂=A₂A₃=…=A₇A₈=1，如果把图2中的直角三角形继续作下去，记OA₁，OA₂，…，OA_n的长度构成的数列为{a_n}，则a₃₆+a₁₆=（　　）

  A．52

  B． 2 13

  C．10

  D．100
  组卷：87引用：2难度：0.8

  解析

三、解答题（本大题共6小题，共85分。解答应写出文字说明，证明过程或演算步骤）

• 20．已知椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右顶点分别为A₁，A₂，上下顶点分别为B₁，B₂，四边形A₁B₁A₂B₂的面积为4，且该四边形内切圆的方程为

  x

  2

  +

  y

  2

  =

  4

  5

  ．
  （1）求椭圆C的方程；
  （2）直线l：y=kx+m（k,m均为常数）与椭圆C相交于M，N两个不同的点（M，N异于A₁，A₂），若以MN为直径的圆过椭圆C的右顶点A₂，试判断直线l能否过定点？若能，求出该定点坐标；若不能，请说明理由．
  组卷：78引用：2难度：0.5

  解析

• 21．将m×n阶数阵

  a 11 ， a 12 ，…， a 1 n

  a 21 ， a 22 ，…， a 2 n

  ⋮ ⋮ ⋮ ⋮

  a m 1 ， a m 2 ，…， a mn

  记作{a_ij}_m×n（其中，当且仅当i=s,j=t时，a_ij=a_st）．如果对于任意的i=1，2，3，…，m,当j₁＜j₂时，都有

  a

  i

  j

  1

  ＜

  a

  i

  j

  2

  ，那么称数阵{a_ij}_m×n具有性质A．
  （Ⅰ）写出一个具有性质A的数阵{a_ij}_3×4，满足以下三个条件：①a₁₁=4，②数列{a_1n}是公差为2的等差数列，③数列{a_m1}是公比为

  1

  2

  的等比数列；
  （Ⅱ）将一个具有性质A的数阵{a_ij}_m×n的每一列原有的各数按照从上到下递增的顺序排列，形成一个新的m×n阶数阵，记作数阵{b_ij}_m×n．试判断数阵{b_ij}_m×n是否具有性质A，并说明理由．
  组卷：63引用：2难度：0.6

  解析