2023年湖北省黄冈市水县兰溪中学中考数学模拟试卷
发布:2024/5/13 8:0:8
一.选择题:(共24分)
-
1.|-2|=( )
组卷:302引用:6难度:0.8 -
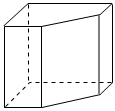 2.如图所示,该几何体的主视图是( )组卷:159引用:3难度:0.8
2.如图所示,该几何体的主视图是( )组卷:159引用:3难度:0.8 -
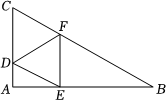 3.如图,Rt△ABC中,∠ABC=30°,AC=1,点D、E分别是边AC、AB上的动点,将DE绕点D逆时针旋转60°,使点E落在边BC的点F处,则EF的最小值是( )组卷:690引用:3难度:0.4
3.如图,Rt△ABC中,∠ABC=30°,AC=1,点D、E分别是边AC、AB上的动点,将DE绕点D逆时针旋转60°,使点E落在边BC的点F处,则EF的最小值是( )组卷:690引用:3难度:0.4 -
4.甲、乙两位同学进行500米短道速滑比赛,他们的五次成绩(单位:秒)如图所示:
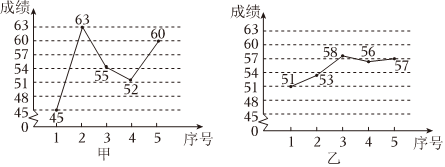
则甲、乙两位同学五次成绩的( )组卷:88引用:4难度:0.7 -
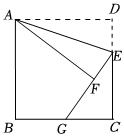 5.如图,正方形ABCD中,AB=12,将△ADE沿AE对折至△AFE,延长EF交BC于点G,G刚好是BC边的中点,则ED的长是( )组卷:219引用:6难度:0.5
5.如图,正方形ABCD中,AB=12,将△ADE沿AE对折至△AFE,延长EF交BC于点G,G刚好是BC边的中点,则ED的长是( )组卷:219引用:6难度:0.5 -
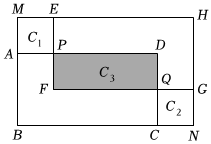 6.如图,将长方形ABCD先向右平移a个单位,再向上平移b个单位,得到长方形EFGH,并使得两个长方形有重叠,延长BA和HE交于点M,延长HG和BC交于点N,构成长方形MBNH.已知AB=6,BC=8.记长方形MAPE,CNGQ和PFQD的周长分别为C1,C2,C3.若C1+C2=24,则C3等于( )组卷:169引用:4难度:0.5
6.如图,将长方形ABCD先向右平移a个单位,再向上平移b个单位,得到长方形EFGH,并使得两个长方形有重叠,延长BA和HE交于点M,延长HG和BC交于点N,构成长方形MBNH.已知AB=6,BC=8.记长方形MAPE,CNGQ和PFQD的周长分别为C1,C2,C3.若C1+C2=24,则C3等于( )组卷:169引用:4难度:0.5 -
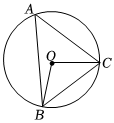 7.如图,⊙O是△ABC的外接圆,若∠A=50°,则∠OBC的度数为( )组卷:101引用:2难度:0.7
7.如图,⊙O是△ABC的外接圆,若∠A=50°,则∠OBC的度数为( )组卷:101引用:2难度:0.7 -
8.二次函数y=x2+bx+c.
①当-1≤x≤1时,y的取值范围是-1≤y≤1,该二次函数的对称轴为直线x=m,则m的最小值为1-.2
②存在实数b和c,使得当-1≤x≤1时,y的取值范围是-1≤y≤1,且y随x增大而增大.
③当-1≤x≤1时,存在函数值y,使得-1≤y≤1.对于任意给定的实数b和c,该函数均有最小值ymin,则ymin的最大值为1.
④若只存在两个自变量值x1,x2,其中-1≤x1<x2≤1,使得对于相应的函数值y1,y2,有-1≤y1≤y2≤1,则该函数最小值为-2.
上述结论中,所有正确结论的序号是( )组卷:199引用:3难度:0.4
三.解答题(共72分)
-
23.在菱形ABCD中,∠DAB=60°,点O为对角线AC的中点,P为线段AC上的一个动点(点P不与点O重合),分别过点A,C向直线BP作垂线AE和CF,垂足分别为点E,F.
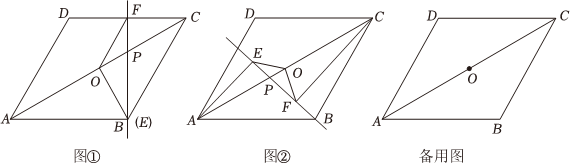
【问题解决】:(1)如图①,当点P在线段OC上,垂足F与CD的中点重合,点E与点B重合时,求证:OE=OF;
【问题探究】:(2)如图②,当点P在线段OA上,OE与OF还相等吗?如果相等,请证明.如果不相等,请说明理由;
【拓展延伸】:(3)当点P在线段AC上运动,∠OEF=30°,猜想线段CF,AE,OE之间有怎样的数量关系?并证明你的猜想.组卷:160引用:4难度:0.1 -
24.已知:如图1,抛物线L:y=ax2-2ax+c(a≠0,c≠0)与y轴交于点C,与x轴交于点A、B两点.
(1)若C点坐标为(0,4),点A的坐标为(4,0);
①求抛物线L的解析式;
②点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积为3时,求点Q的坐标;
(2)若a<0,过抛物线L上第一象限内一定点Q且不平行于坐标轴的直线与抛物线有唯一公共点时,交x轴正半轴于N点,过C点的直线交抛物线于点P,直线PQ:y=kx+b交x轴负半轴于M,如图2,当QM=QN时,k与a之间是否存在某种数量关系?若存在,请写出这个数量关系,并说明理由.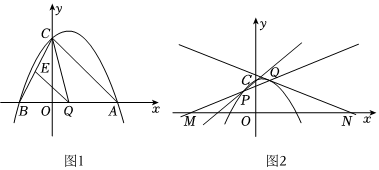 组卷:244引用:4难度:0.2
组卷:244引用:4难度:0.2


