2022-2023学年吉林省长春外国语学校高二（下）月考数学试卷（6月份）

一、单项选择题：本大题共8题，每小题5分，共计40分．每小题列出的四个选项中只有一项是符合题目要求的．

• 1．设集合

  A

  =

  {

  x

  |

  y

  =

  3

  -

  x

  }

  ，

  B

  =

  {

  x

  ∈

  Z

  |

  x

  x

  -

  4

  ≤

  0

  }

  ，则A∩B=（　　）

  A．{x|0≤x＜4}

  B．{x|0≤x≤4}

  C．{x∈N|x＜4}

  D．{x|0≤x≤3}
  组卷：198引用：4难度：0.8

  解析

• 2．已知a∈R，若集合M={1，a}，N={-1，0，1}，则“a=0”是“M⊆N”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：97引用：10难度：0.8

  解析

• 3．某中学高三（1）班有50名学生，在一次高三模拟考试中，经统计得：数学成绩X～N（110，100），则估计该班数学得分大于120分的学生人数为（　　）
  （参考数据：P（|X-μ|＜σ）≈0.68，P（|X-μ|＜2σ）≈0.95．）

  A．16

  B．10

  C．8

  D．2
  组卷：410引用：9难度：0.7

  解析

• 4．6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去1个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有（　　）

  A．120种

  B．90种

  C．60种

  D．30种
  组卷：7525引用：40难度：0.7

  解析

• 5．已知某地区7%的男性和0.49%的女性患色盲．假如男性、女性各占一半，从中随机选一人，则此人恰是色盲的概率是（　　）

  A．0.01245

  B．0.05786

  C．0.02865

  D．0.03745
  组卷：616引用：8难度：0.9

  解析

• 6．若

  （

  x

  -

  1

  2

  ）

  n

  的展开式中第3项的二项式系数是15，则展开式中所有项系数之和为（　　）

  A． 1 32

  B． 1 64

  C． - 1 64

  D． 1 128
  组卷：69引用：9难度：0.9

  解析

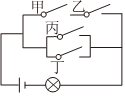• 7．如图，已知电路中4个开关闭合的概率都是

  1

  2

  ，且是相互独立的，则灯亮的概率为（　　）

  A． 1 16

  B． 3 16

  C． 1 4

  D． 13 16
  组卷：193引用：6难度：0.7

  解析

三、解答题：本大题共6小题，共70分．解答应有文字说明、证明过程或演算步骤．

• 21．已知函数f（x）=x²e^2x．
  （1）求曲线y=f（x）在x=1处的切线方程；
  （2）求f（x）的极值．
  组卷：15引用：2难度：0.6

  解析

• 22．高性能计算芯片是一切人工智能的基础．国内某企业已快速启动AI芯片试生产，试产期需进行产品检测，检测包括智能检测和人工检测．智能检测在生产线上自动完成，包括安全检测、蓄能检测、性能检测等三项指标，且智能检测三项指标达标的概率分别为

  49

  50

  ，

  48

  49

  ，

  47

  48

  ，人工检测仅对智能检测达标（即三项指标均达标）的产品进行抽样检测，且仅设置一个综合指标．人工检测综合指标不达标的概率为p（0＜p＜1）．
  （1）求每个AI芯片智能检测不达标的概率；
  （2）人工检测抽检50个AI芯片，记恰有1个不达标的概率为f（p），当p=p₀时，f（p）取得最大值，求p₀；
  （3）若AI芯片的合格率不超过93%，则需对生产工序进行改良．以（2）中确定的p₀作为p的值，试判断该企业是否需对生产工序进行改良．
  组卷：288引用：7难度：0.6

  解析