2021-2022学年江苏省镇江实验高级中学高二（下）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）的一条渐近线与x轴正半轴所成夹角为

  π

  3

  ，则C的离心率为（　　）

  A．2

  B．3

  C． 3

  D． 2 3 3
  组卷：5引用：1难度：0.7

  解析

• 2．已知f（x）=sin2x,那么函数在x=

  π

  2

  处的瞬时变化率为（　　）

  A．1

  B．0

  C．-2

  D．-1
  组卷：19引用：1难度：0.8

  解析

• 3．用数字0，1，2.3，4组成允许有重复数字的三位数，这样的三位数个数为（　　）

  A．125种

  B．100种

  C．64种

  D．60种
  组卷：6引用：1难度：0.7

  解析

• 4．函数f（x）=x²

  +

  2

  x

  的图象为（　　）

  A．

  B．

  C．

  D．
  组卷：3引用：1难度：0.8

  解析

• 5．满足条件A

  2

  n

  ＞C

  3

  n

  的自然数n有（　　）

  A．7个

  B．6个

  C．5个

  D．4个
  组卷：264引用：3难度：0.8

  解析

• 6．过点A（3，5）作圆（x-2）²+（y-3）²=1的切线，则切线的方程为（　　）

  A．x=3或3x+4y-29=0	B．y=3或3x+4y-29=0
  C．x=3或3x-4y+11=0	D．y=3或3x-4y+11=0
  组卷：190引用：4难度：0.7

  解析

• 7．若点A，B分别是函数y=x-4e^x与y=3-3x图象上的动点（其中e是自然对数的底数），则AB的最小值为（　　）

  A． 7 10 10

  B． 49 10

  C． 17

  D．17
  组卷：111引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答时应写出文字说明、证明过程或演算步骤．

• 21．已知a∈R，函数

  f

  （

  x

  ）

  =

  a

  x

  +

  lnx

  -

  1

  ．
  （1）当a=1时，求曲线y=f（x）在点（2，f（2））处的切线方程；
  （2）求f（x）在区间（0，e]上的最小值．
  组卷：177引用：15难度：0.3

  解析

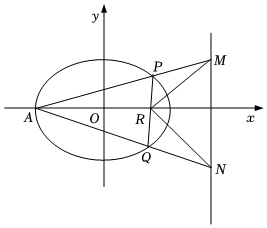• 22．在平面直角坐标系xOy中，椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的离心率为

  1

  2

  ，且过点（2，3）．
  （1）求椭圆C的方程；
  （2）设A为椭圆C的左顶点，过点R（3，0）作与x轴不重合的直线l交椭圆C于P，Q两点，连接AP，AQ分别交直线

  x

  =

  16

  3

  于M，N两点，若直线MR，NR的斜率分别为k₁，k₂，试问k₁k₂是否为定值？若是，求出该定值；若不是，请说明理由．
  组卷：44引用：2难度：0.4

  解析