2021-2022学年重庆市高一（下）调研数学试卷

一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若向量

  OA

  与

  OB

  对应的复数分别是3+2i,-1+4i,则向量

  BA

  对应的复数为（　　）

  A．2+6i

  B．4-2i

  C．-4+2i

  D．4+6i
  组卷：19引用：1难度：0.7

  解析

• 2．下列说法正确的是（　　）

  A．调查长江的水质适合用全面调查

  B．两个互斥事件一定是对立事件

  C．标准差刻画了一组数据的离散程度或波动幅度

  D．若某种奖券的中奖率为0.1，则抽奖10次必有一次中奖
  组卷：9引用：3难度：0.7

  解析

• 3．为做好“新冠肺炎”疫情防控工作，我市各学校坚持落实“双测温两报告”制度，以下是某宿舍6名同学某日上午的体温记录：36.3，36.1，36.4，36.7，36.5，36.6（单位：°C），则该组数据的第80百分位数为（　　）

  A．36.7

  B．36.6

  C．36.5

  D．36.4
  组卷：12引用：2难度：0.8

  解析

• 4．在正方体ABCD-A₁B₁C₁D₁中，E是C₁D₁的中点，则异面直线DE与AC所成角的余弦值为（　　）

  A． 1 20

  B． 10 10

  C． - 10 10

  D． - 1 20
  组卷：190引用：9难度：0.6

  解析

• 5．在梯形ABCD中，AB∥CD且AB=2CD，E为AB上靠近B点处的三等分点，则向量

  EC

  =（　　）

  A． - 1 6 AB + AD

  B． 1 6 AB - AD

  C． 1 6 AB + AD

  D． - 1 6 AB - AD
  组卷：13引用：2难度：0.8

  解析

• 6．袋中有红、黄两种颜色的球各一个，这两个球除颜色外完全相同，从中任取一个，有放回地抽取3次，记事件A表示“3次抽到的球全是红球”，事件B表示“3次抽到的球颜色全相同”，事件C表示“3次抽到的球颜色不全相同”，则下列结论正确的是（　　）

  A．事件A与事件B互斥

  B．事件A与事件C互为对立事件

  C． P （ C ） = 3 4

  D． P （ A ∪ C ） = 3 4
  组卷：14引用：2难度：0.8

  解析

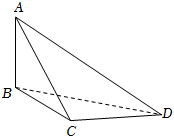• 7．小明同学学以致用，欲测量学校教学楼的高度，他采用了如图所示的方式来进行测量，小明同学在运动场上选取相距25米的C，D两观测点，且C，D与教学楼底部B在同一水平面上，在C，D两观测点处测得教学楼顶部A的仰角分别为45°，30°，并测得∠BCD=120°，则教学楼AB的高度是（　　）

  A．20米

  B．25米

  C．15 3 米

  D．20 2 米
  组卷：101引用：5难度：0.5

  解析

四、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.

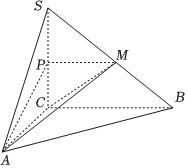• 21．如图，在三棱锥S-ABC中，SC⊥平面ABC，点P，M分别是SC和SB的中点，已知PM=AC=1，∠ACB=90°，直线AM与平面ABC所成的角为30°．
  （1）求证：平面MAP⊥平面SAC；
  （2）求二面角M-AB-C的正切值．
  组卷：8引用：2难度：0.6

  解析

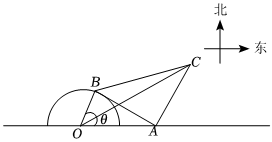• 22．某市为应急处理突如其来的新冠疾病，防止疫情扩散，采取对疑似病人集中隔离观察．如图，征用了该市一半径为2百米的半圆形广场及其东边绿化带设立隔离观察服务区，现决定在圆心O处设立一个观察监测中心（大小忽略不计），在圆心O正东方向相距4百米的点A处安装一套监测设备，为了监测数据更加准确，在半圆弧上的点B以及圆弧外的点C处，再分别安装一套监测设备，且满足AB=AC，∠BAC=90°．定义：四边形OACB及其内部区域为“直接监测覆盖区域”：OC的长为“最远直接监测距离”．设∠AOB=θ．
  （1）求“直接监测覆盖区域”的面积的最大值；
  （2）试确定θ的值，使得“最远直接监测距离”最大．
  组卷：26引用：5难度：0.6

  解析