2022-2023学年湖南师大附中博才实验中学八年级（下）期末数学试卷

一、单选题（10×3=30分）

• 1．下列各图表示y是x的函数的图象是（　　）

  A．	B．
  C．	D．
  组卷：684引用：4难度：0.6

  解析

• 2．一元二次方程x²-4x=5的二次项系数、一次项系数和常数项分别是（　　）

  A．1，4，5

  B．0，-4，-5

  C．1，-4，5

  D．1，-4，-5
  组卷：497引用：6难度：0.5

  解析

• 3．某校八年级进行了三次1000米跑步测试，甲、乙、丙、丁四名同学成绩的方差s²分别为

  s

  2

  甲

  =3.8，

  s

  2

  乙

  =5.5，

  s

  2

  丙

  =10，

  s

  2

  丁

  =6，那么这四名同学跑步成绩最稳定的是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：103引用：6难度：0.7

  解析

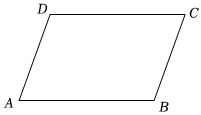• 4．如图，在平行四边形ABCD中，若∠B=2∠A，则∠C的度数为（　　）

  A．60°

  B．45°

  C．120°

  D．135°
  组卷：181引用：4难度：0.7

  解析

• 5．下列各组数中，能构成勾股数的是（　　）

  A．1，1， 2

  B．1， 3 ，2

  C．6，8，10

  D．5，12，15
  组卷：182引用：4难度：0.5

  解析

• 6．已知m是方程x²-3x-1=0的一个根，则代数式2m²-6m的值为（　　）

  A．0

  B．2

  C．-2

  D．4
  组卷：778引用：8难度：0.6

  解析

• 7．下列命题是真命题的是（　　）

  A．对角线相等且互相平分的四边形是矩形

  B．对角线相等的四边形是矩形

  C．平行四边形的对角线互相垂直

  D．对角线互相垂直的四边形是菱形
  组卷：176引用：5难度：0.7

  解析

• 8．我国古代数学家杨辉的《田亩比数乘除减法》中记载：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步？”翻译成数学问题是：一块矩形田地的面积为864平方步，它的宽比长少12步．如果设宽为x步，则可列出方程（　　）

  A．x（x-6）=864	B．x（x-12）=864
  C．x（x+6）=864	D．x（x+12）=864
  组卷：431引用：15难度：0.5

  解析

三、解答题（6+6+6+8+8+9+9+10+10=72分）

• 24．在平面直角坐标系xOy中，点P的坐标为（x₁，y₁），点Q的坐标为（x₂，y₂），且x₁≠x₂，y₁≠y₂，若P，Q为某正方形的两个顶点，且该正方形的边均与某条坐标轴平行（含重合），则称P，Q互为“正方形点”（即点P是点Q的“正方形点”，点Q也是点P的“正方形点”）．下图是点P，Q互为“正方形点”的示意图．
  （1）已知点A的坐标是（2，3），下列坐标中，与点A互为“正方形点”的坐标是

  ．（填序号）
  ①（1，2）；②（-1，5）；③（3，2）．
  （2）若点B（1，2）的“正方形点”C在y轴上，求直线BC的表达式；
  （3）点D的坐标为（-1，0），点M的坐标为（2，m），点N是线段OD上一动点（含端点），若点M，N互为“正方形点”，求m的取值范围．
  组卷：459引用：2难度：0.3

  解析

• 25．已知矩形ABCD中，AB=4，AD=6，点P是边AD的中点．
  （1）如图1，连接BP并延长，与CD的延长线交于点F，问：线段CF上是否存在点Q，使得△PFQ为等腰三角形，若存在，请求出DQ的长，若不存在，请说明理由．
  （2）如图2，把矩形ABCD沿直线MN折叠，使点B落在点D上，直线MN与AD、BD、BC的交点分别为M、H、N，求折痕MN的长．
  （3）如图3，在（2）的条件下，以点A为原点，分别以矩形ABCD的两条边AD、AB所在的直线为x轴和y轴建立平面直角坐标系，若点R在x轴上，在平面内是否存在点S，使以R、M、N、S为顶点的四边形是菱形？若存在，请直接写出点S的坐标；若不存在，请说明理由．
  （4）如图4，若点E为CD边上的一个动点，连结PE，以PE为边向下方作等边△PEG，连结AG，则AG的最小值是

  ．（请直接写出答案）
  
  组卷：973引用：2难度：0.1

  解析