2023年江苏省苏州市工业园区景城学校中考数学二模试卷

一、选择题：本大题共8小题，每小题3分，共24分，在每小题所给出的四个选项中，只有一项是符合题目要求的.请将选择题的答案用2B铅笔涂在答题卡相应位置上.

• 1．下列实数中，是无理数的是（　　）

  A．3.1415926	B．1-π
  C．1.010010001	D．cos60°
  组卷：37引用：1难度：0.8

  解析

• 2．刚刚发布的2023年全国主要城市第一季度GDP排行榜中，苏州市以5186.6亿元排名全国第七位，其中5186.6亿用科学记数法可表示为（　　）

  A．5.1866×1012	B．0.51866×1012
  C．5.1866×1011	D．51.866×1010
  组卷：71引用：1难度：0.8

  解析

• 3．下列运算正确的是（　　）

  A．（a3）4=a12	B．（-2a）2=-4a2
  C．a3•a3=a9	D．a6÷a2=a3
  组卷：227引用：5难度：0.7

  解析

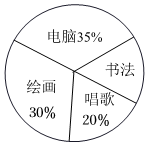• 4．如图是某校七年级学生参加课外兴趣小组的扇形统计图（每人只参加一项），若参加书法兴趣小组的人数是30人，则参加绘画兴趣小组的人数是（　　）

  A．36人

  B．40人

  C．60人

  D．200人
  组卷：765引用：6难度：0.7

  解析

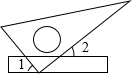• 5．如图，将一块直角三角板的直角顶点放在直尺的一边上．若∠2=40°，则∠1的度数是（　　）

  A．60°

  B．50°

  C．40°

  D．30°
  组卷：655引用：18难度：0.7

  解析

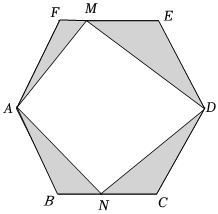• 6．如图是面积为6的正六边形ABCDEF飞镖游戏板，点M，N分别为边EF，BC上的一点，若向该六边形飞镖游戏板投掷一枚飞镖，假设飞镖击中正六边形内的每一个位置是等可能的（击中图中阴影部分的边界或没有击中正六边形板，则重投一次），任意投掷飞镖一次，飞镖击中图中阴影部分的概率是（　　）

  A． 1 3

  B． 1 2

  C． 2 3

  D． 5 6
  组卷：262引用：3难度：0.5

  解析

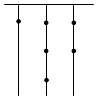• 7．在我国远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”，类似现在我们熟悉的“进位制”．如图所示是远古时期一位母亲记录孩子自出生后的天数，在从右向左依次排列的不同绳子上打结，满五进一，根据图示可知，孩子已经出生的天数是（　　）

  A．27

  B．42

  C．55

  D．210
  组卷：1121引用：16难度：0.7

  解析

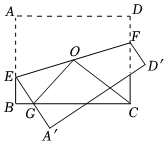• 8．如图，在矩形ABCD中，AB=6，BC=8．点O为矩形ABCD的对称中心，点E为边AB上的动点，连接EO并延长交CD于点F．将四边形AEFD沿着EF翻折，得到四边形A′EFD′，边A′E交边BC于点G，连接OG、OC，则△OGC的面积的最小值为（　　）

  A．18-3 7

  B． 9 2 +3 7

  C．12- 3 7 2

  D．6+ 3 7 2
  组卷：1163引用：7难度：0.4

  解析

二、填空题：本大题共8小题，每小题3分，共24分.把答案直接填写在答题卡相应位置上.

• 9．在函数y=

  2

  x

  -

  1

  中，自变量x的取值范围是

  ．
  组卷：1928引用：265难度：0.7

  解析

三、解答题：本大题共11小题，共82分.把解答过程写在答题卡相应位置上，解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B铅笔或黑色墨水签字笔.

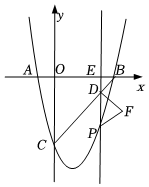• 26．如图，已知抛物线y=ax²+bx-8与x轴交于点A（-2，0），B（8，0）两点，与y轴交于点C，点P是直线BC下方抛物线上一动点，过点P作直线PE∥y轴，交直线BC于点D，交x轴于点F，以PD为斜边，在PD的右侧作等腰直角△PDF．
  （1）求抛物线的表达式，并直接写出直线BC的表达式；
  （2）设点P的横坐标为m（0＜m＜3），在点P运动的过程中，当等腰直角△PDF的面积为9时，请求出m的值；
  （3）连接AC，该抛物线上是否存在一点M，使∠ACO+∠BCM=∠ABC，若存在，请直接写出所有符合条件的点M的坐标，若不存在，请说明理由．
  组卷：555引用：3难度：0.2

  解析

• 27．【材料阅读】在等腰三角形中，我们把底边与腰长的比叫做顶角的张率（scop）．如图1，在△XYZ中，XY=XZ，顶角X的张率记作scop∠X=

  底边

  腰

  =

  YZ

  XY

  ．容易知道一个角的大小与这个角的张率也是相互唯一确定的，所以，类比三角函数，我们可按上述方式定义∠α（0°＜∠α＜180°） 的张率，例如，scop60°=1，scop90°=

  2

  ，请根据材料，完成以下问题：
  如图2，P是线段AB上的一动点（不与点A，B重合），点C，D分别是线段AP，BP的中点，以AC，CD，DB为边分别在AB的同侧作等边三角形△ACE，△CDF，△DBG，连接PE和PG．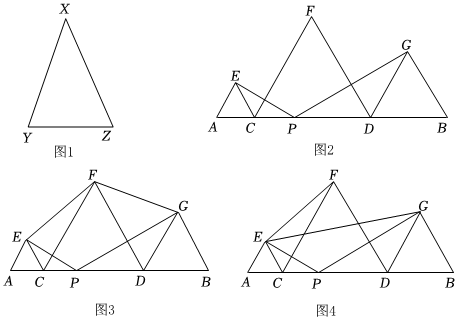
  
  （1）【理解应用】
  ①若等边三角形△ACE，△CDF，△DBG的边长分别为a,b,c,则a,b,c三者之间的关系为

  ；
  ②scop∠EPG=

  ；
  （2）【猜想证明】如图3，连接EF，FG，猜想scop∠EFG的值是多少，并说明理由；
  （3）【拓展延伸】如图4，连接EF，EG，若AB=12，

  EF

  =

  2

  7

  ，则△EPG的周长是多少？此时AP的长为多少？（可直接写出上述两个结果）
  组卷：976引用：2难度：0.1

  解析