2022-2023学年河南省信阳市高一(下)期末数学试卷
发布:2024/8/5 8:0:8
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合A=
,则B∩∁UA=( ){x|(x+1)(x-5)≥0},B={x|y=log24-x}组卷:73引用:3难度:0.7 -
2.设f(x)是周期为3的奇函数,当-1≤x<0时,f(x)=2x2-1,则
等于( )f(72)组卷:103引用:3难度:0.7 -
3.在平面直角坐标系xOy中,
,i分别是与x轴、y轴方向相同的单位向量,已知j=OA,i+2j,OB=3i+4j,若OC=2ti+(t+5)j与AB共线,则实数t的值为( )AC组卷:335引用:3难度:0.7 -
4.函数
在区间(2,4)上存在零点.则实数m的取值范围是( )f(x)=log2x+x2+m组卷:377引用:10难度:0.7 -
5.当x>a时,
的最小值为10,则a=( )2x+8x-a组卷:381引用:2难度:0.7 -
6.在三棱锥P-ABC中,PA⊥平面ABC,PA=6,BC=3,∠CAB=
,则三棱锥P-ABC的外接球的表面积为( )π6组卷:103引用:2难度:0.5 -
7.一组样本数据x1,x2,…,xn的平均数为
,标准差为s.另一组样本数据xn+1,xn+2,…,x2n的平均数为x(x≠0),标准差为s.两组数据合成一组新数据x1,x2,…,xn,xn+1,…,x2n,新数据的平均数为3x,标准差为s',则( )y组卷:163引用:4难度:0.7
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
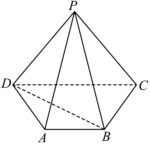 21.如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,且PC=PD=5,AB∥CD,CD=8,DA=AB=BC=4.
21.如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,且PC=PD=5,AB∥CD,CD=8,DA=AB=BC=4.
(1)求证:BD⊥PA;
(2)求二面角A-BD-P的余弦值.组卷:208引用:3难度:0.5 -
22.已知向量
.a=(cosx,-1),b=(3sinx,1),函数f(x)=(a+b)•a-12
(I)求函数f(x)的单调增区间.
(2)若方程上有解,求实数m的取值范围.3[f(x)]2-f(x)+m=0在x∈(0,π2)
(3)设,已知区间[a,b](a,b∈R且a<b)满足:y=g(x)在[a,b]上至少含有100个零点,在所有满足上述条件的[a,b]中求b-a的最小值.g(x)=f(x+π12)-12组卷:291引用:5难度:0.4


