2023-2024学年山西省长治市部分学校九年级（上）月考数学试卷（9月份）

一、选择题（本大题共10个小题，每小题3分，共30分）

• 1．若

  （

  m

  -

  2

  ）

  x

  m

  2

  -

  2

  -

  mx

  +

  1

  =

  0

  是一元二次方程，则m的值为（　　）

  A．2

  B．-2

  C． 2

  D． - 2
  组卷：1097引用：13难度：0.7

  解析

• 2．抛物线y=-2（x+1）²-6的顶点坐标为（　　）

  A．（-1，6）

  B．（1，-6）

  C．（1，6）

  D．（-1，-6）
  组卷：805引用：9难度：0.7

  解析

• 3．一元二次方程x²-2x+a=0的一根是3，则另外一根是（　　）

  A．3

  B．1

  C．-3

  D．-1
  组卷：679引用：6难度：0.8

  解析

• 4．二次函数y=2x²-3x-c（c＞0）的图象与x轴的交点情况是（　　）

  A．有1个交点

  B．有2个交点

  C．无交点

  D．无法确定
  组卷：1621引用：12难度：0.8

  解析

• 5．用配方法解方程x²+8x+7=0，则配方正确的是（　　）

  A．（x+4）2=9

  B．（x-4）2=9

  C．（x-8）2=16

  D．（x+8）2=57
  组卷：5849引用：188难度：0.9

  解析

• 6．已知抛物线y=-x²+2x+c,若点（0，y₁）（1，y₂）（3，y₃）都在该抛物线上，则y₁、y₂、y₃的大小关系是（　　）

  A．y3＞y1＞y2

  B．y3＜y2＜y1

  C．y3＞y2＞y1

  D．y3＜y1＜y2
  组卷：1616引用：15难度：0.5

  解析

• 7．若k＜0，则关于x的一元二次方程x²+x+k-1=0根的情况是（　　）

  A．有两个不相等的实数根	B．没有实数根
  C．有两个相等的实数根	D．只有一个实数根
  组卷：976引用：19难度：0.9

  解析

三、解答题（本大题共8个小题，共75分）解答应写出文字说明，证明过程或演算步骤.

• 22．在一块长16m、宽12m的矩形荒地上，要建造一个花园，要求花园所占面积为荒地面积的一半．方案一：如图1，花园四周小路的宽度相等；方案二：如图2，矩形中每个角上的扇形相同．
  
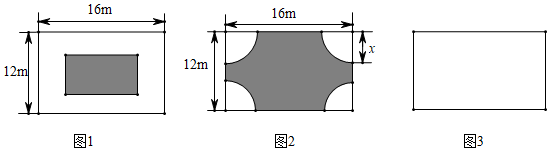
  （1）求方案一中小路的宽度，设小路的宽度为x米，请列出方程，不做解答．
  （2）求方案二中扇形的半径；（其中π≈3，结果保留根号）
  （3）你还有其他的设计方案吗？请在图3中画出你的设计草图，将花园部分涂上阴影，并加以说明．
  组卷：708引用：8难度：0.5

  解析

• 23．如图，抛物线

  y

  =

  -

  1

  2

  x

  2

  +

  mx

  +

  n

  与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（-1，0），C（0，2）．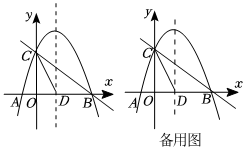
  ​
  （1）求抛物线的解析式；
  （2）点E是线段BC上的一个动点（不与B、C重合），过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时点E的坐标．
  （3）在抛物线的对称轴上是否存在点P，使△PCD为等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由．
  组卷：537引用：5难度：0.3

  解析