当前位置：试卷中心 > 试卷详情

2023年贵州省铜仁市碧江区中考数学模拟试卷（3月份）

发布：2024/5/11 8:0:9

一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置作答，每小3分，共36分.

1．在-1，-2，0，
9
这四个数中，最小的数是（　　）
A．-1 B．-2 C．0 D．
9
组卷：21引用：1难度：0.7
解析
2．下列图案中，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：79引用：3难度：0.5
解析
3．据统计，2023年铜仁市中考学生人数约5.8万左右，用科学记数法表示“5.8万”正确的是（　　）
A．5.8×10² B．58×10³ C．5.8×10³ D．5.8×10⁴
组卷：8引用：2难度：0.8
解析

4．下列说法正确的是（　　）

A．随机抛掷硬币10次，一定有5次正面向上

B．一组数据8，9，10，11，11的众数是10

C．为了了解某电视节目的收视率，宜采用抽样调查

D．甲、乙两射击运动员分别射击10次，他们成绩的方差分别为S_甲²=4，S_乙²=9，在这过程中，乙发挥比甲更稳定

组卷：18引用：2难度：0.6

解析

5．以方程组
y
=
2
x
-
5
y
=
-
x
+
1
的解为坐标的点（x,y）在平面直角坐标系中的位置是（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：216引用：4难度：0.5
解析
6．如图是一个几何体的三视图，主视图和左视图均是面积为12的等腰三角形，俯视图是直径为6的圆，则这个几何体的全面积是（　　）
A．24π B．21π C．15π D．12π
组卷：395引用：7难度：0.5
解析
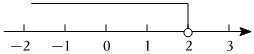7．一个不等式的解集在数轴上表示如图，则这个不等式可以是（　　）
A．2x＜0 B．2x≥4 C．x-4＜2 D．4-x＞2
组卷：176引用：8难度：0.7
解析
8．将二次函数y=-（x-k）²+k+1的图象向右平移1个单位，再向上平移2个单位后，顶点在直线y=2x+2上，则k的值为（　　）
A．2 B．1 C．0 D．-1
组卷：183引用：1难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：本大题共9小题，共98分解答应写出必要的文字说明、证明过程或演算步骤.

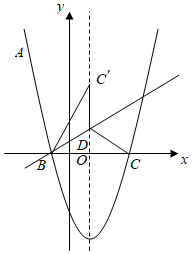24．如图，抛物线y=ax²+bx+c经过点A（-2，5），与x轴相交于B（-1，0），C（3，0）两点．
（1）求抛物线的函数表达式；
（2）点D在抛物线的对称轴上，且位于x轴的上方，将△BCD沿直线BD翻折得到△BC'D，若点C'恰好落在抛物线的对称轴上，求点C'和点D的坐标；
（3）设P是抛物线上位于对称轴右侧的一点，点Q在抛物线的对称轴上，当△CPQ为等边三角形时，求直线BP的函数表达式．
组卷：6156引用：8难度：0.2
解析
25．【问题提出】如图1，在Rt△ABC中，∠ACB=90°，点E，F分别为边AC，BC的中点，将△EFC绕点C顺时针旋转α（0°＜α＜360°），连接AE，BF，试探究AE，BF之间存在怎样的数量关系和位置关系？

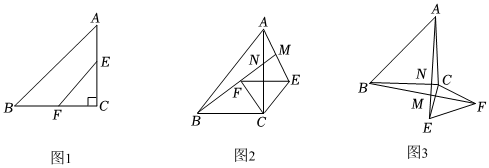
【特例探究】若AC=BC，将△EFC绕点C顺时针旋转至图2的位置，直线BF与AE，AC分别交于点M，N．按以下思路完成填空（第一个空填推理依据，第二个空填数量关系，第三个空填位置关系）：
∵AC=BC，点E，F分别为边AC，BC的中点，
∴CE=CF．
∵∠ACB=∠ECF，
∴∠ACE=∠BCF．
∴△ACE≌△BCF（
）．
∴AE
BF，∠CAE=∠CBF．
又∵∠ANM=∠BNC，
∴∠AMN=∠BCN=90°．
∴AE
BM．
【猜想证明】若BC=nAC（n＞1），△EFC绕点C顺时针旋转至图3的位置，直线AE与BF，BC分别交于点M，N，猜想AE与BF之间的数量关系与位置关系，并就图3所示的情况加以证明；
【拓展运用】若AC=4，BC=6，将△EFC绕点C顺时针旋转α（0°＜α＜360°），直线AE与BF相交于点M，当以点C，E，M，F为顶点的四边形是矩形时，请直接写出BM的长．
组卷：55引用：3难度：0.5
解析