2022-2023学年四川省眉山市部分名校高一（下）联考数学试卷（5月份）

一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知全集U={x∈N^*|x＜6}，集合A={1，3}，B={2，3，4}，则A∩（∁_UB）=（　　）

  A．{1}

  B．{3}

  C．∅

  D．{1，3}
  组卷：151引用：3难度：0.9

  解析

• 2．若复数

  z

  =

  i

  2

  2

  +

  3

  i

  ，则

  z

  =（　　）

  A． 2 13 + 3 13 i

  B． 2 13 - 3 13 i

  C． - 2 13 + 3 13 i

  D． - 2 13 - 3 13 i
  组卷：48引用：4难度：0.8

  解析

• 3．已知向量

  a

  =

  （

  -

  2

  ，

  7

  ）

  ，

  b

  =

  （

  m

  2

  -

  5

  ，

  m

  +

  15

  ）

  ，且

  a

  ∥

  b

  ，则m=（　　）

  A．1或 - 7 5

  B．1或 - 5 7

  C．-1或 7 5

  D．-1或 5 7
  组卷：34引用：2难度：0.8

  解析

• 4．若

  tan

  （

  θ

  -

  3

  π

  ）

  =

  5

  2

  ，则

  sin

  （

  π

  +

  θ

  ）

  +

  cos

  （

  π

  -

  θ

  ）

  sin

  （

  π

  2

  +

  θ

  ）

  +

  2

  cos

  （

  π

  2

  -

  θ

  ）

  =（　　）

  A． - 7 12

  B． - 3 8

  C． - 7 8

  D． - 1 4
  组卷：157引用：2难度：0.7

  解析

• 5．某火锅店开张第一周进店消费的人数逐日增加，设第x（1≤x≤7，x∈N）天进店消费的人数为y,且y与

  [

  7

  x

  3

  3

  +

  3

  x

  ]

  （[t]表示不大于t的最大整数）成正比，假设第2天有6人进店消费，则第3天进店消费的人数为（　　）

  A．12

  B．15

  C．18

  D．20
  组卷：17引用：2难度：0.5

  解析

• 6．“

  |

  tanα

  |

  =

  1

  2

  ”是“

  |

  lo

  g

  3

  tan

  （

  α

  +

  π

  4

  ）

  |

  =

  1

  ”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：20引用：2难度：0.8

  解析

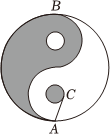• 7．如图，在太极图中，大圆半径是小圆半径的6倍，A，B分别为太极图中的最低点和最高点，过A作黑色小圆的切线，切点为C，则向量

  AB

  在向量

  AC

  上的投影向量为（　　）

  A． 6 AC

  B． 4 AC

  C． 4 2 AC

  D． 3 2 AC
  组卷：11引用：2难度：0.6

  解析

四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知函数

  f

  （

  x

  ）

  =

  lg

  4

  x

  ，g（x）=log₂（ax+1）．
  （1）若函数y=1-g（x）在[1，2]内有唯一零点，求a的取值范围．
  （2）设函数φ（x）的最大值、最小值分别为M，m,记D[φ（x）]=M-m.设a=2，函数φ（x）=g（x）-log₂x,当x∈[1，t₁]，

  t

  2

  ∈

  [

  1

  10

  ，

  10

  ]

  时，D[φ（x）]＞D[f（t₂）]恒成立，求t₁的取值范围．
  组卷：41引用：5难度：0.5

  解析

• 22．已知CD为△ABC中AB边上的中线，

  AD

  =

  1

  ，

  ∠

  BCD

  =

  1

  2

  ∠

  CAD

  ．
  （1）若BC=2，求CD的长；
  （2）若

  CD

  =

  2

  AD

  ，求AC²+BC²的值及AC³+4AC²-AC的值．
  组卷：29引用：4难度：0.5

  解析