2022-2023学年江西省鹰潭市高一(下)期末数学试卷
发布:2024/6/9 8:0:9
一、单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.下列说法正确的是( )
组卷:109引用:5难度:0.8 -
2.已知向量
,a=(4,-2),若b=(x-1,2),则a⊥b=( )|a-b|组卷:555引用:5难度:0.8 -
3.已知角
,且角θ的终边所在直线经过点θ=2023π3,则x的值为( )P(x,23)组卷:77引用:2难度:0.9 -
4.北极阁位于鹰潭公园的东侧,前门是大码头,旧时为鹰潭最繁华的街市.某同学为测量北极阁的高度MN,在北极阁的正北方向找到一座建筑物AB,高约为30m,在地面上点C处(B,C,N三点共线)测得建筑物顶部A,北极阁顶部M的仰角分别为30°和45°,在A处测得北极阁顶部M的仰角为15°,北极阁的高度约为( )
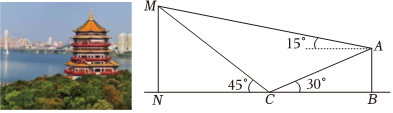 组卷:40引用:1难度:0.6
组卷:40引用:1难度:0.6 -
5.将复数
对应的向量1+3i绕原点按顺时针方向旋转ON,得到的向量为π2,那么ON1对应的复数是( )ON1组卷:64引用:3难度:0.8 -
6.关于θ,对于甲、乙、丙、丁四人有不同的判断,甲:θ是第三象限角,乙:
.丙:tan2θ>1,丁:tan(θ-π)不小于2,若这人只有一人判断错误,则此人是( )tanθ=12组卷:113引用:8难度:0.8 -
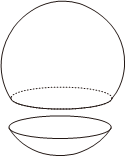 7.一个球体被平面截下的一部分叫做球缺.截面叫做球缺的底面,垂直于截面的直径被截后,剩下的线段长叫做球缺的高,球缺曲面部分的面积S=2πRH,其中R为球的半径,H为球缺的高.如图,若一个半径为R的球体被平面所截获得两个球缺,其高之比为,则表面积(包括底面)之比H1H2=3=( )S1S2组卷:24引用:1难度:0.6
7.一个球体被平面截下的一部分叫做球缺.截面叫做球缺的底面,垂直于截面的直径被截后,剩下的线段长叫做球缺的高,球缺曲面部分的面积S=2πRH,其中R为球的半径,H为球缺的高.如图,若一个半径为R的球体被平面所截获得两个球缺,其高之比为,则表面积(包括底面)之比H1H2=3=( )S1S2组卷:24引用:1难度:0.6
四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.在△ABC中,内角A,B,C所对的边分别为a,b,c,且
.bsinA=asin(B+π3)
(1)求角B的大小;
(2)若a=3,c=2,求b和sin(A-C)的值.组卷:252引用:6难度:0.5 -
22.向量是解决数学问题的有力工具,我们可以利用向量探究△ABC的面积问题:
(1)已知|AB|=2,|AC|=5,,求△ABC的面积;AB•AC=8
(2)已知不共线的两个向量,AB=(x1,y1),探究△ABC的面积表达式;AC=(x2,y2)
(3)已知O(0,0),若抛物线y=x2-2x-3上两点A(x1,y1)、B(x2,y2)满足x2=x1+1,求△OAB面积的最小值.组卷:16引用:3难度:0.5


