2022-2023学年广东省梅州市丰顺县大龙华学校九年级（上）月考数学试卷（9月份）

一、选择题（共10题，共30分）

• 1．既是中心对称图形又是轴对称图形，且只有两条对称轴的四边形是（　　）

  A．正方形

  B．矩形

  C．菱形

  D．矩形或菱形
  组卷：586引用：13难度：0.9

  解析

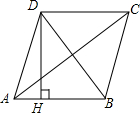• 2．如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（　　）

  A． 24 5

  B． 12 5

  C．5

  D．4
  组卷：14362引用：100难度：0.5

  解析

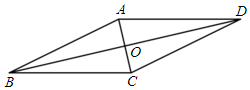• 3．如图，▱ABCD的对角线AC、BD交于点O，顺次连接▱ABCD各边中点得到一个新的四边形，如果添加下列四个条件中的一个条件：①AC⊥BD；②C_△ABO=C_△CBO；③∠DAO=∠CBO；④∠DAO=∠BAO，可以使这个新的四边形成为矩形，那么这样的条件个数是（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：1631引用：5难度：0.7

  解析

• 4．在矩形ABCD中，AB=6，AD=8，P是AD上一动点，PE⊥AC于E，PF⊥BD于F，则PE+PF的值为（　　）

  A．4

  B．4.4

  C．4.8

  D．5
  组卷：191引用：4难度：0.9

  解析

• 5．如图，在△ABC中，∠CAB=90°，AB=AC=4，P为AC中点，点D在直线BC上运动，以AD为边，向AD的右侧作正方形ADEF，连接PF，则在点D的运动过程中，线段PF的最小值为（　　）

  A．2

  B． 2

  C．1

  D． 2 2
  组卷：687引用：4难度：0.6

  解析

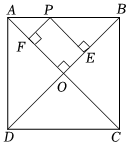• 6．如图，在正方形ABCD中，AC与BD相交于点O，AB=2cm,点P为AB上任意一点，PE⊥OB于点E，PF⊥OA于点F，则PE+PF的值为（　　）

  A．2cm

  B． 2 cm

  C．2 2 cm

  D．1cm
  组卷：12引用：2难度：0.5

  解析

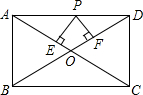
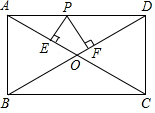• 7．已知：如图，矩形ABCD中，AB=5，BC=12，对角线AC、BD相交于点O，点P是线段AD上任意一点，且PE⊥AC于点E，PF⊥BD于点F，则PE+PF等于（　　）

  A． 60 13

  B． 50 13

  C． 18 5

  D． 12 5
  组卷：1546引用：6难度：0.6

  解析

• 8．如图，点P的坐标为（2，2），点A，B分别在x轴，y轴的正半轴上运动，且∠APB=90°，下列结论：
  ①PA=PB；
  ②当OA=OB时四边形OAPB是正方形；
  ③四边形OAPB的面积和周长都是定值；
  ④连接OP，AB，则AB＞OP，其中正确的有（　　）

  A．①②

  B．①②③

  C．①②④

  D．①②③④
  组卷：455引用：5难度：0.4

  解析

三、解答题（共8小题，满分62分）

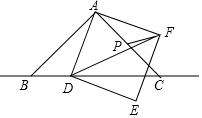
• 24．数学课上，李老师出示了如下的题目：
  “在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC，如图，试确定线段AE与DB的大小关系，并说明理由”．
  小敏与同桌小聪讨论后，进行了如下解答：
  （1）特殊情况，探索结论
  当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE

  DB（填“＞”，“＜”或“=”）．
   （2）特例启发，解答题目
  解：题目中，AE与DB的大小关系是：AE

  DB（填“＞”，“＜”或“=”）．理由如下：如图2，过点E作EF∥BC，交AC于点F．（请你完成以下解答过程）
  （3）拓展结论，设计新题
  在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长（请你直接写出结果）．
  
  组卷：11977引用：39难度：0.3

  解析

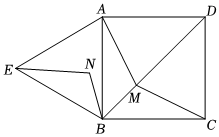• 25．如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．
  （1）证明：△ABM≌△EBN．
  （2）当M点在何处时，AM+BM+CM的值最小，并说明理由．
  （3）当AM+BM+CM的值最小值为

  3

  +1时，则正方形的边长为

  ．
  组卷：1103引用：3难度：0.1

  解析