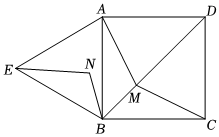
如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．
（1）证明：△ABM≌△EBN．
（2）当M点在何处时，AM+BM+CM的值最小，并说明理由．
（3）当AM+BM+CM的值最小值为3+1时，则正方形的边长为 22．
3
2
2
【考点】四边形综合题．
【答案】
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/9 8:0:9组卷：1104引用：3难度：0.1
相似题
-
1．如图，四边形ABCD、EBGF都是正方形．
（1）如图1，若AB=4，EC=，求FC的长；17
（2）如图2，正方形EBGF绕点B逆时针旋转，使点G正好落在EC上，猜想AE、EB、EC之间的数量关系，并证明你的结论；
（3）如图3，在（2）条件下，∠BCE=22.5°，EC=2，点M为直线BC上一动点，连接EM，过点M作MN⊥EC，垂足为点N，直接写出EM+MN的最小值．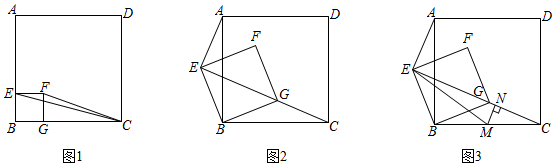
发布：2025/5/24 19:0:1组卷：233引用：2难度：0.5 -
2．如图1，在菱形ABCD中，AB=10，∠BAD=α（0°＜α＜180°），连接AC，点Q是AD上的一点，连接BQ交AC于点E，过点E作EG⊥AD于点G，连接DE．
（1）当α=60°且时，DQAQ=12=，DG=；DEEQ
（2）当时，若S菱形ABCD=50时．求DG的长度；DQAQ=1
（3）当时，如图2，分别以点E，A为圆心，大于DQAQ=1为半径画弧．交于点F和H，作直线FH，分别交AB，AC，AD于点P，N，M，请你判断点M的位置是否变化？若不变，求AM的长；若变化说明理由．12AE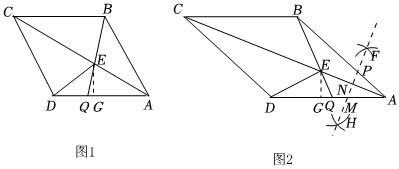
发布：2025/5/24 19:0:1组卷：88引用：4难度：0.3 -
3．如图，在正方形ABCD中，AB=6，E为AB的中点，连结CE，作CF⊥EC交射线AD于点F，过点F作FG∥CE交射线CD于点G，连结EG交AD于点H．
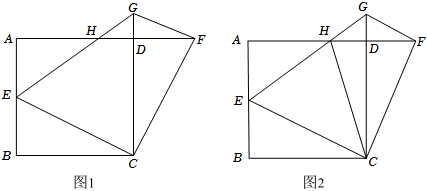
（1）求证：CE=CF．
（2）求HD的长．
（3）如图2，连结CH，点P为CE的中点，Q为AF上一动点，连结PQ，当∠QPC与四边形GHCF中的一个内角相等时，求所有满足条件的DQ的长．发布：2025/5/24 18:0:1组卷：789引用：2难度：0.1
