2022-2023学年湖北省新高考协作体高二(下)联考数学试卷(3月份)
发布:2024/7/6 8:0:9
一、单选题(共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案填涂在答题卡相应位置上)
-
1.数列
,-12×1,12×2,-12×3,⋯的通项公式为( )12×4组卷:174引用:3难度:0.8 -
2.已知抛物线C:y2=2px(p>0)上一点M(3,m)(m>0)到其焦点F的距离等于4,则直线MF的倾斜角为( )
组卷:57引用:1难度:0.6 -
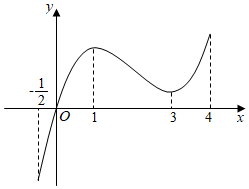 3.定义在区间上的函数f(x)的导函数f'(x)的图象如图所示,则下列结论正确的是( )[-12,4]组卷:581引用:8难度:0.7
3.定义在区间上的函数f(x)的导函数f'(x)的图象如图所示,则下列结论正确的是( )[-12,4]组卷:581引用:8难度:0.7 -
4.在等比数列{an}中,a3,a7是函数
的极值点,则a5=( )f(x)=13x3-4x2+4x-1组卷:566引用:9难度:0.5 -
5.正方形的面积及周长都随着边长的变化而变化,则当正方形的边长为3cm时,面积关于周长的瞬时变化率为( )
组卷:50引用:3难度:0.8 -
6.正项数列{an}的前n项和为Sn,且S5=10,S10=50,若直线l:3x+4y+an-1+an+1-3=0(n∈N*)与圆C:(x-1)2+y2=
相切,则S15=( )425a2n(an>0)组卷:37引用:3难度:0.6 -
7.高斯(Gauss)被认为是历史上最重要的数学家之一,并享有“数学王子”之称.小学进行1+2+3+⋯+100的求和运算时,他这样算的:1+100=101,2+99=101,…,50+51=101,共有50组,所以50×101=5050,这就是著名的高斯算法,课本上推导等差数列前n项和的方法正是借助了高斯算法.已知正数数列{an}是公比不等于1的等比数列,且a1a2023=1,试根据以上提示探求:若
,则f(a1)+f(a2)+⋯+f(a2023)=( )f(x)=41+x2组卷:139引用:7难度:0.6
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
-
21.已知正项数列{an}的前n项和为Sn,且
.2Sn=an+1
(1)证明:{an}是等差数列;
(2)设数列的前n项和为Tn,若满足不等式Tn<m的正整数n的个数为3,求m的取值范围.{Snanan+1}组卷:139引用:4难度:0.5 -
22.已知函数f(x)=(x-a)lnx-x+a-3(a∈R)
(1)若a=0,求f(x)的极小值;
(2)讨论函数f′(x)的单调性;
(3)当a=2时,λ≤f(x)恒成立,求λ的最大整数值.组卷:18引用:2难度:0.6


