2022-2023学年福建省厦门市集美实验学校九年级(上)期中数学试卷
发布:2024/9/26 9:0:2
一、选择题(本大题有10个小题,每个小题4分,共40分)
-
1.下列图标中,既是轴对称图形,又是中心对称图形的是( )
组卷:569引用:9难度:0.7 -
2.下列方程中,是关于x的一元二次方程的是( )
组卷:16引用:2难度:0.5 -
3.已知二次函数y=3(x-1)2+5,下列结论正确的是( )
组卷:445引用:14难度:0.7 -
4.将一元二次方程x2-8x+10=0通过配方转化为(x+a)2=b的形式,下列结果中正确的是( )
组卷:1868引用:37难度:0.6 -
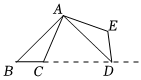 5.如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )组卷:2773引用:67难度:0.9
5.如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )组卷:2773引用:67难度:0.9 -
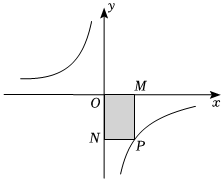 6.如图,过双曲线上任意一点P分别作x轴,y轴的垂线PM,PN,交x轴、y轴于点M、N,所得矩形PMON的面积为8,则k的值是( )组卷:22引用:2难度:0.7
6.如图,过双曲线上任意一点P分别作x轴,y轴的垂线PM,PN,交x轴、y轴于点M、N,所得矩形PMON的面积为8,则k的值是( )组卷:22引用:2难度:0.7 -
7.用一条长40cm的绳子怎样围成一个面积为75cm2的矩形?设矩形的一边为x米,根据题意,可列方程为( )
组卷:652引用:7难度:0.7 -
8.如图选项中,能描述函数y=ax2+b与y=ax+b,(ab<0)的图象可能是( )
组卷:1463引用:9难度:0.7
三、解答题(本大题有9题,共86分)
-
24.将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.
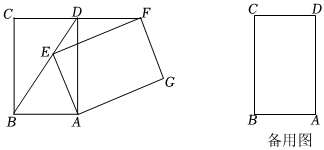
(1)如图,当点E在BD上时.求证:∠BDA=∠DEF;
(2)当α为何值时,GC=GB?画出图形.并说明理由.组卷:44引用:2难度:0.5 -
25.如图,在平面直角坐标系中,抛物线y=-x2-2x+c(c为常数)与一次函数y=-x+b(b为常数)交于A、B两点,其中A点坐标为(-3,0).
(1)求B点坐标;
(2)点P为直线AB上方抛物线上一点,连接PA,PB,当S△PAB=时,求点P的坐标;1258
(3)将抛物线y=-x2-2x+c(c为常数)沿射线AB平移5个单位,平移后的抛物线y1与原抛物线y=-x2-2x+c相交于点E,点F为抛物线y1的顶点,点M为y轴上一点,在平面直角坐标系中是否存在点N,使得以点E,F,M,N为顶点的四边形是菱形,若存在,请直接写出点N的坐标;若不存在,请说明理由.2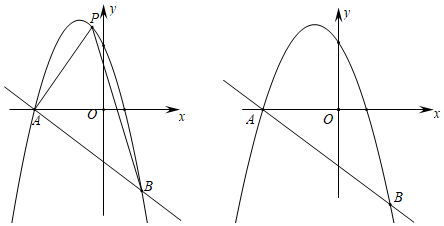 组卷:486引用:5难度:0.1
组卷:486引用:5难度:0.1


