2021-2022学年江苏省无锡第一女子中学八年级(上)期中数学试卷
发布:2024/9/17 3:0:8
一、选择题:(每题3分,共30分,把正确选项前的字母代号填在题后的括号内)
-
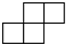 1.下列图形中,和所给图全等的图形是( )组卷:1787引用:17难度:0.9
1.下列图形中,和所给图全等的图形是( )组卷:1787引用:17难度:0.9 -
2.下列各组数,可以作为直角三角形的三边长的是 ( )
组卷:131引用:11难度:0.7 -
3.已知等腰三角形的一个内角等于100°,则它的顶角是( )
组卷:28引用:2难度:0.8 -
4.下列图形中,是轴对称图形的是( )
组卷:24引用:2难度:0.7 -
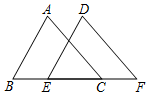 5.如图,若△ABC≌△DEF,BC=6,EC=4,则CF的长为( )组卷:424引用:3难度:0.7
5.如图,若△ABC≌△DEF,BC=6,EC=4,则CF的长为( )组卷:424引用:3难度:0.7 -
6.如果等腰三角形有两边长为5和8,那么该三角形的周长为( )
组卷:441引用:3难度:0.7 -
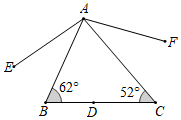 7.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF,根据图中标示的角度,∠EAF的度数为( )组卷:849引用:10难度:0.7
7.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF,根据图中标示的角度,∠EAF的度数为( )组卷:849引用:10难度:0.7 -
8.下列所给的四组条件中,能作出唯一三角形的是( )
组卷:495引用:8难度:0.7
三、解答题:(共74分,解答时应写明演算步骤、证明过程或必要的文字说明)
-
25.木工师傅为了让直尺经久耐用,常常在直尺的直角顶点与斜边之间加一个小木条,如图所示.右图为其示意图.若∠BAC=90°,线段AB的长为5,线段AC的长为12,试求出小木条AD的最短长度.
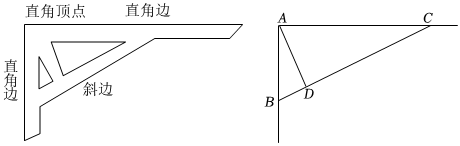 组卷:99引用:4难度:0.5
组卷:99引用:4难度:0.5 -
26.阅读理解:
【问题情境】
教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?
【探索新知】
从面积的角度思考,不难发现:
大正方形的面积=小正方形的面积+4个直角三角形的面积
从而得数学等式:;(用含字母a、b、c的式子表示)
化简证得勾股定理:a2+b2=c2
【初步运用】
(1)如图1,若b=2a,则小正方形面积:大正方形面积=;
(2)现将图1中上方的两直角三角形向内折叠,如图2,若a=4,b=6此时空白部分的面积为;
【迁移运用】
如果用三张含60°的全等三角形纸片,能否拼成一个特殊图形呢?带着这个疑问,小丽拼出图3的等边三角形,你能否仿照勾股定理的验证,发现含60°的三角形三边a、b、c之间的关系,写出此等量关系式及其推导过程.
知识补充:如图4,含60°的直角三角形,对边y:斜边x=定值k.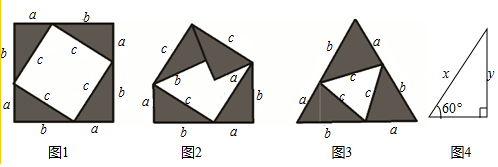 组卷:1814引用:10难度:0.4
组卷:1814引用:10难度:0.4


