当前位置：试卷中心 > 试卷详情

2023-2024学年广东省珠海市香洲区梅华中学九年级（上）期中数学试卷

发布：2024/10/2 11:0:4

一、选择题（每题3分，共30分）

1．下列图形中，是中心对称图形的是（　　）
A． B． C． D．
组卷：68引用：2难度：0.8
解析
2．下列方程是关于x的一元二次方程的是（　　）
A．x+2y=1 B．x²+x-1=x² C．
x
2
+
3
x
=
8
D．x²-5x=0
组卷：334引用：8难度：0.9
解析
3．方程x²-x+9=0根的情况是（　　）
A．有实根 B．有两个相等的实数根
C．无实根 D．有两个不相等的实数根
组卷：28引用：3难度：0.5
解析
4．把抛物线y=2x²先向左平移3个单位，再向上平移4个单位，所得抛物线的函数表达式为（　　）
A．y=2（x+3）²+4 B．y=2（x+3）²-4
C．y=2（x-3）²-4 D．y=2（x-3）²+4
组卷：2974引用：69难度：0.9
解析
5．用配方法解方程x²-8x+1=0时，配方结果正确的是（　　）
A．（x-4）²=5 B．（x-4）²=16 C．（x-4）²=7 D．（x-4）²=15
组卷：218引用：7难度：0.7
解析
6．点P₁（-1，y₁），P₂（3，y₂），P₃（5，y₃）均在二次函数y=-x²+2x+3的图象上，则y₁、y₂、y₃的大小关系是（　　）
A．y₃＞y₂＞y₁ B．y₃＞y₁=y₂ C．y₁＞y₂＞y₃ D．y₁=y₂＞y₃
组卷：502引用：6难度：0.6
解析
7．等腰三角形两边长为方程x²-7x+10=0的两根，则它的周长为（　　）
A．12 B．12或9 C．9 D．7
组卷：542引用：15难度：0.9
解析
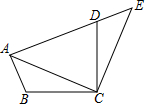8．如图，将△ABC绕点C顺时针旋转90°得到△EDC．若点A，D，E在同一条直线上，∠ACB=20°，则∠ADC的度数是（　　）
A．55° B．60° C．65° D．70°
组卷：8099引用：100难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

五、解答题（每题12分，共24分）

23．已知，四边形ABCD是正方形，△DEF绕点D旋转（DE＜AB），∠EDF=90°，DE=DF，连接AE，CF．

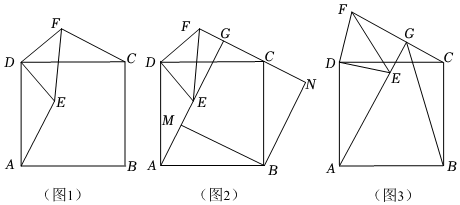
（1）如图1，线段AE与线段CF的关系是
，并说明理由；已知直线AE与CF相交于点G；
（2）如图2，BM⊥AG于点M，BN⊥CF于点N，求证：四边形BMGN是正方形；
（3）如图3，连接BG，若AB=2，DE=1，在△DEF旋转的过程中，线段BG长度的最小值是
．
组卷：539引用：3难度：0.5
解析
24．综合与探究
如图：抛物线y=ax²-2x+c经过点A（-6，0），B（2，0）两点，与y轴交于点C，连接AC．

（1）求抛物线的函数表达式，并直接写出对称轴l的表达式．
（2）点P是直线AC上方抛物线上的一个动点．
①在对称轴l上是否存在点D，使得以点A、P、D为顶点的三角形为等腰直角三角形，若存在，求出点P的坐标；若不存在，请说明理由．
②在y轴上是否存在点E与点P关于直线AC对称，若存在，请直接写出点E的坐标；若不存在，请说明理由．
组卷：201引用：2难度：0.1
解析