2022-2023学年四川省达州市开江县八年级（下）期末数学试卷

一、选择题（共10小题）

• 1．中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录，下列四幅作品分别代表“清明”、“谷雨”、“白露”、“大雪”，其中是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：670引用：23难度：0.9

  解析

• 2．下列从左至右的变形，因式分解正确的是（　　）

  A．2b2-8b=b（2b-8）	B． x 2 - xy + 1 4 y 2 = （ x - 1 2 y ） 2
  C．-a2+b2=（-a+b）（-a-b）	D． a 2 + 2 = a （ a + 2 a ）
  组卷：67引用：1难度：0.6

  解析

• 3．把不等式组

  1 2 x ＞ - 3

  x - 3 ≥ 10

  中每个不等式的解集在同一条数轴上表示出来，正确的为（　　）

  A．	B．
  C．	D．
  组卷：25引用：2难度：0.8

  解析

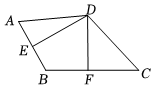• 4．如图，DE，DF分别是线段AB，BC的垂直平分线，连接DA，DC，则（　　）

  A．∠A=∠C

  B．∠B=∠ADC

  C．DA=DC

  D．DE=DF
  组卷：1279引用：8难度：0.8

  解析

• 5．从①AB∥CD；②BC∥AD；③BC=AD；④AB=CD这四个条件中选取两个，使四边形ABCD成为平行四边形．下面条件不能说明四边形ABCD是平行四边形的是（　　）

  A．①②

  B．③④

  C．②④

  D．②③
  组卷：29引用：1难度：0.5

  解析

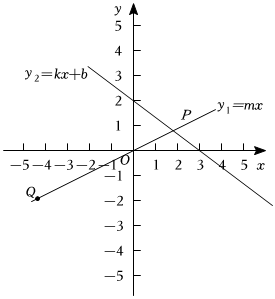• 6．如图，直线y₁=mx经过P（2，1）和Q（-4，-2）两点，且与直线y₂=kx+b交于点P，则不等式kx+b＜mx的解集为（　　）

  A．x＞2

  B．x＜2

  C．x＞-4

  D．x＜-4
  组卷：18引用：1难度：0.5

  解析

• 7．在平面直角坐标系中，将点A（5，2）先向右平移3个单位长度，再向下平移5个单位长度得到点A′，则点A′的坐标为（　　）

  A．（3，5）

  B．（2，-3）

  C．（2，7）

  D．（8，-3）
  组卷：15引用：1难度：0.6

  解析

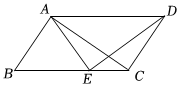• 8．如图，在▱ABCD中，E为BC边上一点，且AB=AE，∠B=55°，∠EAC=20°，则∠CED的度数为（　　）

  A．35°

  B．30°

  C．25°

  D．20°
  组卷：180引用：1难度：0.5

  解析

三、解答题（共10小题）

• 24．阅读材料：若m²-2mn+2n²-8n+16=0，求m、n的值．
  解：∵m²-2mn+2n²-8n+16=0，
  ∴（m²-2mn+n²）+（n²-8n+16）=0，
  ∴（m-n）²+（n-4）²=0，
  ∴（m-n）²=0，（n-4）²=0，
  ∴n=4，m=4．
  根据你的理解，探究下面的问题：
  （1）已知x²-4xy+5y²+6y+9=0，求x²y-xy²的值．
  （2）已知等腰三角形ABC的三边长是a、b、c,且满足a²+b²-8a-18b+97=0，求△ABC的周长．
  （3）已知a²+b²=16，ab+c²-16c+72=0，求（a-b）²+c²的值．
  组卷：76引用：1难度：0.5

  解析

• 25．【问题背景】
  在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，试探究图1中线段BE、EF、FD之间的数量关系．
  【初步探索】
  小亮同学认为：延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，则可得到BE、EF、FD之间的数量关系是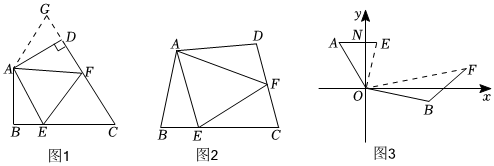

  ．
  
  【探索延伸】
  在四边形ABCD中如图2，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，∠EAF=

  1

  2

  ∠BAD，上述结论是否仍然成立？说明理由．
  【结论运用】
  如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角（∠EOF）为70°，试求此时两舰艇之间的距离．
  组卷：142引用：4难度：0.5

  解析