2023-2024学年福建省厦门一中高三（上）第一次月考数学试卷（10月份）
发布：2024/9/1 0:0:9
一、选择题：本题8小题，每题5分，共40分.在每题给出的四个选项中只有一项是符合题目要求的.
-
1．已知集合A={0，1，2，3}，B={x|x=n2-1，n∈A}，P=A∪B，则P的子集共有（ ）
组卷：734引用：8难度：0.7 -
2．若（1+i）z=2i,其中i为虚数单位，则
=（ ）zz组卷：52引用：2难度：0.8 -
3．已知函数f（x）的定义域为[1，+∞），数列{an}满足an=f（n），则“数列{an}为递增数列”是“函数f（x）为增函数”的（ ）
组卷：130引用：5难度：0.8 -
4．如图所示，九连环是中国传统民间智力玩具，以金属丝制成9个圆环，解开九连环共需要256步，解下或套上一个环算一步，且九连环的解下和套上是一对逆过程．九连环把玩时按照一定得程序反复操作，可以将九个环全部从框架上解下或者全部套上．将第n个圆环解下最少需要移动的次数记为an（n≤9，n∈N*），已知a1=1，a2=1，按规则有an=an-1+2an-2+1（n≥3，n∈N*），则解下第5个圆环最少需要移动的次数为（ ）组卷：78引用：1难度：0.5 -
5．用一个平行于圆锥C底面的平面截该圆锥得到一个圆台，若圆台上底面和下底面半径之比为
，则该圆台与圆锥C的体积之比为（ ）23组卷：74引用：2难度：0.7 -
6．已知角α的终边落在直线y=-2x上，则2cos2α+sin2α+3sin2α的值为（ ）
组卷：76引用：2难度：0.7 -
7．已知双曲线
的左、右焦点分别为F1、F2，过F2作一条直线与双曲线右支交于A、B两点，坐标原点为O，若|OA|=x2a2-y2b2=1（a＞0，b＞0），|BF1|=5a,则该双曲线的离心率为（ ）a2+b2组卷：188引用：2难度：0.5
四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
-
21．某工厂A，B两条相互独立的生产线生产同款产品，在产量一样的情况下通过日常监控得知，A，B生产线生产的产品为合格品的概率分别为p和2p-1（0.5≤p≤1）．
（1）从A，B生产线上各抽检一件产品，若使得至少有一件合格的概率不低于99.5%，求p的最小值p0．
（2）假设不合格的产品均可进行返工修复为合格品，以（1）中确定的p0作为p的值．
①已知A，B生产线的不合格品返工后每件产品可分别挽回损失5元和3元，若从两条生产线上各随机抽检1000件产品，以挽回损失的平均数为判断依据，估计哪条生产线的挽回损失较多？
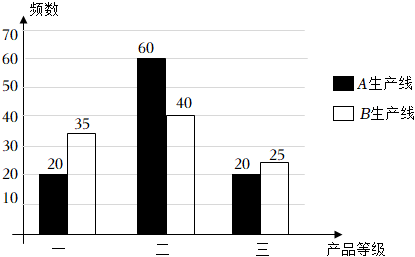
②若最终的合格品（包括返工修复后的合格品）按照一、二、三等级分类后，每件可分别获利10元、8元、6元，现从A，B生产线的最终合格品中各随机抽取100件进行检测，结果统计如图：用样本的频率分布估计总体分布，记该工厂生产一件产品的利润为X，求X的分布列并估计该厂产量2000件时利润的期望值．组卷：205引用：9难度：0.8 -
22．函数f（x）=sinx-ax+1．
（1），求f（x）的单调区间；a=12
（2）若f（x）≥cosx在x∈[0，π]上恒成立，求实数a的取值范围；
（3）令函数g（x）=f（x）+ax-1，求证：．g（π15）+g（2π15）+g（3π15）+…+g（8π15）≥225组卷：319引用：3难度：0.1
